Osebne zbirke


Paralelogram je večkotnik s štirimi stranicami.
Nasproti si stoječi stranici v paralelogramu sta vzporedni, na kar lahko sklepamo že iz njegovega imena (paralelno pomeni vzporedno). Na sliki vidimo paralelogram. Ima dva para vzporednih stranic, ki ležita nasproti.
Kot smo že povedali, ima paralelogram dva para vzporednih stranic. Vzporedni stranici ležita nasproti.
Za stranice paralelograma velja:
ima dva para vzporednih stranic,
vzporedni stranici ležita nasproti,
vzporedni stranici sta enake dolžine.
Ker ima paralelogram vzporedne stranice, ima tudi več parov skladnih kotov, tako notranjih kot zunanjih.
V naslednjem primeru bodimo pozorni na krake kotov, ki ležijo na nosilkah stranic paralelograma. Ker sta nasprotni stranici paroma vzporedni, imajo tudi koti paroma vzporedne krake.
Za kote paralelograma velja:
Nasprotna kota sta skladna.
Sosednja notranja kota sta sokota (njuna vsota meri 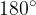 ).
).
Notranji kot oglišča in zunanji kot sosednjega oglišča sta skladna.
Tako kot v vsakem štirikotniku je vsota velikosti tako notranjih kot zunanjih kotov paralelograma enaka 360 stopinj.
Višino paralelograma lahko opišemo na dva načina:
kot daljico, ki poteka pravokotno med nosilkama nasproti ležečih stranic,
oziroma kot razdaljo med nosilkama nasproti ležečih stranic.
Drugi opis je nam pride prav pri načrtovanju paralelogramov s podano višino.
Kot vemo, razdaljo med daljicama (oziroma njenima nosilkama) merimo pravokotno na daljici, zato je tudi višina vedno pravokotna na nasproti si stoječi stranici.
Ker ima paralelogram dva para vzporednih stranic, ima tudi dve višini.
Višino lahko narišemo kjerkoli med nosilkama vzporednih stranic. Nahaja se lahko deloma ali v celoti znotraj ali zunaj paralelograma.
Zunaj jo običajno narišemo, kadar je kakšna stranica zelo kratke dolžine.
Paralelogram ima tako kot vsak štirikotnik dve diagonali. Označimo jih z malima črkama e in f.
V paralelogramu se diagonali razpolavljata.
Tako kot vsem geometrijskim likom tudi paralelogramu lahko določimo najbolj značilni količini, obseg in ploščino:
Pri obsegu se ukvarjamo z merjenjem dolžine sklenjene črte, ki omejuje paralelogram.
Pri ploščini pa z določanjem velikosti dela ravnine znotraj te sklenjene črte.
Obseg merimo v dolžinskih merskih enotah. Osnovna merska enota za dolžino je meter.
Ploščino merimo v ploščinskih merskih enotah. Osnovna merska enota za ploščino je kvadratni meter.
Obseg paralelograma predstavlja vsoto vseh stranic. V enačbi upoštevamo, da sta po dve in dve stranici enako dolgi.
Obseg paralelograma izračunamo po obrazcu:
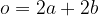
pri čemer sta a in b dolžini stranic.
Ploščina paralelograma predstavlja velikost dela ravnine, ki ga omejuje sklenjena lomljena črta, sestavljena iz njegovih stranic. Izračunamo jo po naslednjem obrazcu.
Ploščino paralelograma izračunamo po obrazcu:
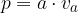
pri čemer je a poljubna stranica paralelograma, 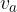 pa višina na to stranico.
pa višina na to stranico.
Gornjo enačbo za izračun ploščine lahko izpeljemo tako, da paralelogram preoblikujemo v pravokotnik.
Paralelogram lahko poljubno zasukamo. Zato lahko njegovo ploščino izračunamo s katerokoli stranico in višino na to stranico:
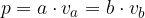
Paralelogram načrtujemo na podlagi poznavanja konstrukcije osnovnih geometrijskih elementov in kotov.
Za konstrukcijo paralelograma potrebujemo tri neodvisne podatke. Ti podatki so kombinacija:
stranic
notranjih kotov
višin in
diagonal.
Pred vsako konstrukcijo paralelograma narišemo skico, ki nam služi za orientacijo pri risanju. Na skici po možnosti označimo vsak podatek s svojo barvo.
Naloge za načrtovanje paralelograma na grobo razdelimo v tri skupine:
načrtovanje s podanimi stranicami in koti,
načrtovanje s podanimi stranicami, koti in višinami,
načrtovanje s podanimi stranicami, koti, višinami in diagonalami.
V nadaljevanju bomo za vsako skupino rešili en primer naloge.
Pri teh nalogah sta običajno podani obe stranici ter kot 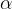 ali kot
ali kot 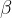 .
.
Pri teh nalogah je lahko podano:
Stranici a in b ter višina na eno izmed njih, ali
kot 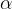 ali
ali 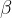 ter obe višini (tako na stranico a kot na stranico b), ali
ter obe višini (tako na stranico a kot na stranico b), ali
kot 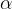 ali
ali 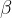 , stranica a ali b ter višina na podano stranico.
, stranica a ali b ter višina na podano stranico.
Oglejmo si primer za zadnjo od opisanih kombinacij.
Pri teh nalogah obstaja veliko kombinacij s podanimi tremi od omenjenih podatkov, oglejmo si primer s podanima stranicama ter eno izmed diagonal.