Prijava z e-naslovom
Prijava brez gesla
Večkotniki so geometrijski liki, ki ležijo v ravnini. Vsi geometrijski liki so omejeni s sklenjeno črto, ki sama sebe ne seka.
Pri večkotnikih je ta sklenjena črta sestavljena iz več krajših ravnih črt, ki ne ležijo na isti premici. Enako kot velja za ostale geometrijske like, pa mora biti ta črta sklenjena. Imenujemo jo lomljenka.
Za večkotnike je značilno, da jih omejuje sklenjena enostavna lomljenka.
Lomljenka je črta, sestavljena iz več zaporednih daljic, ki ne ležijo na isti premici.
To, da je lomljenka sklenjena, pomeni, da se zaključi sama vase. Začne in konča se torej v isti točki.
To, da je lomljenka enostavna, pomeni, da črta nikjer ne prečka same sebe. Daljice, ki jo sestavljajo, se torej ne sekajo.
Večkotniki so sestavljeni iz osnovnih gradnikov geometrije v ravnini.
Točke, na katerih se lomljena ravna črta lomi, imenujemo oglišča geometrijskega lika. Odseke med zaporednimi oglišči pa imenujemo stranice geometrijskega lika.
Kot smo povedali, lomljenko sestavlja več zaporednih daljic. V večkotniku vsako tako daljico imenujemo stranica, krajišča stranic pa so oglišča večkotnika.
Oglišča označimo z velikimi tiskanimi črkami, stranice pa z malimi tiskanimi črkami.
Poseben primer večkotnikov je pravilni večkotnik. Zanj je značilno, da ima vse:
stranice enake dolžine in
kote skladne.
Notranji kot ima vrh v oglišču večkotnika, njegova kraka pa potekata skozi sosednji oglišči.
Vsak notranji kot večkotnika ima pripadajoč zunanji kot, s katerim si delita vrh, ki leži v istem oglišču. Zunanji kot je sokot notranjega kota oziroma tisti kot, ki notranjemu manjka do 180 stopinj.
Kot smo povedali, sosednji oglišči povezuje stranica. Če je to mogoče, lahko povežemo tudi nesosednji oglišči. Tako daljico pa imenujemo diagonala.
Diagonala je daljica, ki povezuje nesosednji oglišči večkotnika.
Zakaj smo zgoraj zapisali "če je to mogoče"? Oglejmo si naslednji primer.
Diagonalo torej lahko vrišemo le večkotniku, ki ima vsaj 4 oglišča.
Večkotnike lahko glede na lastnosti delimo na več načinov. V nadaljevanju bomo spoznali dve najpogostejši delitvi:
glede na število stranic in
glede na vbočenost in izbočenost.
Večkotnike po številu stranic delimo na:
trikotnik (3 stranice),
štirikotnik (4 stranice),
petkotnik (5 stranic),
oziroma splošno n-kotnik z n stranicami.
Govorimo o stranicah, medtem, ko se v imenih večkotnikov skriva beseda "kot". Zakaj?
Oglejmo si naslednji primer, v katerem vidimo povezavo med številom stranic, oglišč in notranjih kotov.
Glede na ugotovitev lahko splošno rečemo, da večkotnik lahko poimenujemo tako po številu stranic kot tudi po številu oglišč ali notranjih kotov.
Večkotnike glede na velikost notranjih kotov delimo na:
izbočene (konveksne) in
vbočene (konkavne).
V izbočenem večkotniku so vsi notranji koti manjši od 180°.
V vbočenem večkotniku je vsaj en notranji kot večji od 180°.
V nadaljevanju se bomo osredotočili na izbočene večkotnike.
Oglišča označimo po vrsti po abecednem redu.
Če si črke sledijo v nasprotni smeri gibanja urinih kazalcev, je pravokotnik pozitivno orientiran.
Če si črke sledijo v smeri gibanja urinih kazalcev, je pravokotnik negativno orientiran.
Določene lastnosti večkotnikov lahko tudi izračunamo. V nadaljevanju si jih bomo nekaj ogledali.
Vsako oglišče v n-kotniku ima dve sosednji oglišči, ostala oglišča pa so nesosednja. Število diagonal, ki jih lahko narišemo iz enega oglišča, torej dobimo tako, da od vseh oglišč odštejemo tri oglišča - dve sosednji in oglišče samo.
Izraz za izračun števila diagonal iz enega oglišča se glasi:
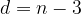
pri čemer n pomeni število oglišč večkotnika.
Število vseh diagonal pa dobimo tako, da število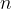 
oglišč množimo s številom 
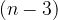diagonal iz enega oglišča. Ker pa vsaka izmed diagonal povezuje dve oglišči, bi tako vsako diagonalo šteli dvakrat. Zato moramo rezultat deliti z 2.
Izraz za izračun števila vseh diagonal v večkotniku se glasi:
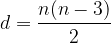
pri čemer n pomeni število oglišč večkotnika.
V večkotniku obstaja naslednja povezava med notranjim in zunanjim kotom:
Vsota notranjega in zunanjega kota večkotnika je enaka 180 stopinj.
Notranji in zunanji kot večkotnika sta sokota.
Vsota notranjih kotov je odvisna od števila oglišč večkotnika.
Izraz za izračun vsote notranjih kotov v večkotniku se glasi:
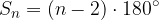
pri čemer n pomeni število oglišč večkotnika.
Vsota zunanjih kotov v večkotniku pa je vedno enaka:
Vsota zunanjih kotov v poljubnem večkotniku znaša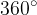 
.
