Prijava z e-naslovom
Prijava brez gesla
Pitagorov izrek je posebno pravilo, ki velja samo v pravokotnem trikotniku. V vsakem pravokotnem trikotniku imamo dve pravokotni kateti in najdaljšo stranico, hipotenuzo:
Pravokotni trikotnik z oznakami.
Izrek pravi, da je vsota kvadratov dolžin katet, ki oklepata pravi kot, enaka kvadratu dolžine hipotenuze, ki leži nasproti pravemu kotu v pravokotnem trikotniku:
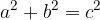
Najdaljša stranica v pravokotnem trikotniku se imenuje hipotenuza. Krajši stranici pa se imenujeta kateti.
Ni nujno, da stranice pravokotnega trikotnika označimo s črkami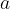 
, 
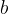in 
. Oznake stranic so odvisne od tega, kako imamo označena oglišča trikotnika. Če oglišča niso označena potem lahko uporabimo katerokoli črko angleške abecede.
Lastnosti pravokotnega trikotnika:
Najdaljša stranica pravokotnega trikotnika se imenuje hipotenuza in vedno leži nasproti pravemu kotu.
En krak pravega kota v pravokotnem trikotniku je ena kateta, drugi krak pravega kota v pravokotnem trikotniku je druga kateta. Kateti torej oklepata pravi kot.
Vsota kotov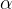 
in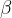 
ob hipotenuzi je enaka 90 kotnih stopinj.
Ploščina pravokotnega trikotnika je enaka polovičnem produktu katet:
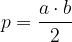
Pitagorov izrek je eden izmed najbolj znanih izrekov v pravokotnem trikotniku. Če poznamo dve stranici pravokotnega trikotnika, potem lahko izračunamo tretjo stranico. Za računanje neznane stranice uporabljamo ali obliko s kvadrati ali brez kvadratov.
Tri ekvivalentne enačbe Pitagorovega izreka:
To poglavje z dokazom izreka je navedeno za popestritev. Sicer pa ga lahko učenci brez škode preskočijo, saj presega osnovnošolski nivo.
Poglejmo si geometrijski dokaz Pitagorovega izreka. Primerjajmo dve sliki enako velikega kvadrata, v katerem vidimo po štiri enake pravokotne trikotnike:
Dva različna razreza enakega kvadrata.
Iz slike je očitno, da sta ploščini levega in desnega kvadrata enaki:
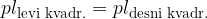
Iz zapisane enakosti lahko izpeljemo Pitagorov izrek:
Dobili smo enačbo, ki predstavlja Pitagorov izrek in je obenem dokaz, da izrek res velja v pravokotnem trikotniku. Ne glede na to, kakšni sta dolžini katet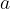 
in 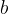na gornjih trikotnikih, vedno dobimo, da je vsota kvadratov teh dveh katet enaka kvadratu hipotenuze . Zato lahko sklepamo, da to pravilo (Pitagorov izrek) velja za vsak pravokotni trikotnik.
Trojice naravnih števil, ki predstavljajo stranice pravokotnih trikotnikov, se imenujejo pitagorejske trojice. Takšnih trojic obstaja neskončno mnogo.
Poglejmo še nekaj drugih pitagorejskih trojic, urejenih v tabeli:
Če vsako izmed števil v eni trojici pomnožimo istim številom, potem spet dobimo pitagorejsko trojico. Tudi nova števila predstavljajo stranice pravokotnega trikotnika.
V nadaljevanju bomo videli, kako Pitagorov izrek uporabimo pri reševanju nalog z različnimi geometrijskimi liki. Če želimo uporabiti Pitagorov izrek, potem moramo znotraj nekega geometrijskega lika opaziti pravokotni trikotnik.
Kvadrat je geometrijski lik, ki ga omejujeta štiri enako dolge stranice, velikost njegovih notranjih kotov pa je 90 stopinj.
Za kvadrat je značilno, da ga ena ali druga diagonala razdeli na dva skladna pravokotna trikotnika.
Za primer, kako uporabimo Pitagorov izrek v kvadratu, poglejmo en pravokotni trikotnik, ki ga dobimo, ko narišemo diagonalo kvadrata.
Zdaj že znamo izpeljati formulo za izračun diagonale v kvadratu.
V kvadratu izračunamo diagonalo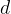 
s pomočjo formule:
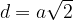
Diagonala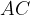 
razdeli pravokotnik na dva skladna pravokotna trikotnika. Zato lahko uporabimo Pitagorov izrek za izračun diagonale ali ene od stranic, če poznamo drugi dve dolžini.
Diagonalo v pravokotniku izračunamo z enačbo:
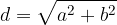
Enakostranični trikotnik je geometrijski lik, omejen s tremi enako dolgimi stranicami.
Enakostranični trikotnik
Višina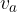 
enakostranični trikotnik razdeli na dva skladna pravokotna trikotnika. Višina obenem razpolovi tudi osnovnico. Zaradi tega pri uporabi Pitagorovega izreka potrebujemo samo en podatek za računanje dolžine stranice ali višine.
Če se osredotočimo na enega izmed teh dveh pravokotnih trikotnikov, potem vidimo, da je stranica 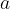enakostraničnega trikotnika hipotenuza, polovica stranice 
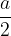je ena kateta in višina 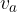druga kateta.
V enakostraničnem trikotniku izračunamo višino s formulo:
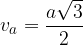
Višina na osnovnico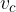 
razdeli enakokraki trikotnik na dva ploščinsko enaka pravokotna trikotnika.
V enakokrakem trikotniku velja 
Razrežimo enakokraki trikotnik na dve enaki polovici:
Zapišimo Pitagorov izrek za polovico enakokrakega trikotnika (glej gornjo sliko):
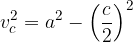
Višino na osnovnico v enakokrakem trikotniku izračunamo z:
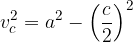
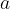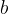Enakokraki trapez ima osnovnici in vzporedni, kraka in 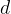pa enako dolga.
Enakokraki trapez; 
in 
Pokažimo nekaj možnosti uporabe Pitagorovega izreka. Ugotoviti torej moramo, kje v enakokrakem trapezu lahko najdemo pravokotne trikotnike.
Prvi primer pravokotnega trikotnika
Najdemo lahko pravokotni trikotnik s kateto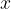 
, hipotenuzo 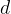in drugo kateto 
:
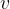Dolžino 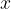bi lahko izračunali s Pitagorovim izrekom ali pa tako, da od osnovnice 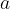odštejemo osnovnico in rezultat delimo z 2:
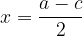
V nadaljevanju so ekvivalentne enačbe, ki jih lahko uporabimo v enakokrakem trapezu. Kraka enakokrakega trapeza sta obenem tudi hipotenuzi pravokotnih trikotnikov, ki jih lahko najdemo v enakokrakem trapezu:
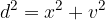
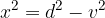
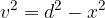
V enakokrakem trapezu izračunamo višino z enačbo:
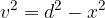
Drugi primer pravokotnega trikotnika
Pravokotni trikotnik tvorijo tudi višina, diagonala in del osnovnice:
Diagonalo 
v enakokrakem trapezu izračunamo z enačbo:
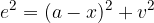
Kateto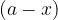 
v enakokrakem trapezu izračunamo s preurejeno enačbo:
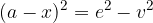
Višino v enakokrakem trapezu, če poznamo diagonalo in 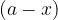, pa izračunamo z enačbo:
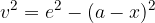
V enakokrakem trapezu izračunamo diagonalo z enačbo:
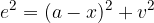
Romb ima vse štiri stranice enako dolge, diagonali pa se sekata pod pravim kotom in se razpolavljata.
Diagonali in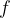 
razdelita romb na štiri skladne pravokotne trikotnike. Polovični diagonali sta kateti pravokotnih trikotnikov, stranica romba pa je hipotenuza.
Pitagorov izrek v rombu lahko uporabimo, če poznamo stranico in eno izmed diagonal ali pa dolžini obeh diagonal.
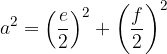
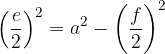
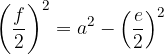
V rombu izračunamo stranico 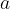s pomočjo diagonal z enačbo:
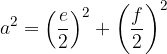
Ker se v deltoidu diagonali in 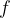sekata pravokotno, lahko uporabimo Pitagorov izrek. Poglejmo podrobneje en pravokotni trikotnik.
Iz gornje slike lahko zapišemo tri enakovredne enačbe Pitagorovega izreka.
Stranico 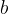izračunamo z enačbo:
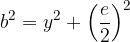
Diagonalo izračunamo s pomočjo enačbe:
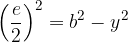
Del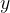 
diagonale 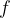izračunamo z enačbo:
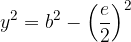
V deltoidu izračunamo stranico 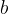s pomočjo diagonal z enačbo:
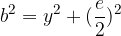
Koordinatni sistem je ogrodje, v katerem lahko z uporabo Pitagorovega izreka hitro in natančno izračunamo razdaljo med dvema točkama oziroma dolžino neke daljice.
Poglejmo, kako ugotovimo razdaljo med točkama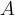 
in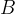 
.
Najprej narišemo daljico s krajišči 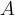in .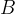
Iz točke 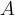narišemo pravokotnico na vodoravno os koordinatnega.
Iz točke 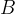narišemo pravokotnico na navpično os koordinatnega sistema.
Presečišče pravokotnic označimo s točko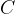 
.
Vidimo, da smo dobili pravokotni trikotnik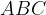 
. Zato lahko v njemu uporabimo Pitagorov izrek za izračun razdalje med točkama 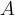in .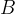
Pri tem sta stranici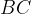 
in 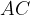kateti. Stranica 
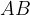pa je hipotenuza.
Dolžina stranice 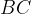je enaka razliki med 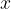koordinatama točk 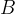in :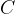
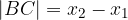
Dolžina stranice 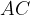je enaka razliki med 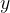koordinatama točk 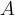in :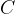
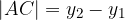
Pitagorov izrek z dolžinami stranic zapišemo:
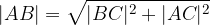
S točkami in koordinatami pa tako:
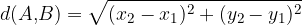
V pravokotnem koordinatnem sistemu poznamo koordinate točk, zato lahko razdaljo med poljubnima točkama 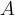in 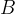izračunamo s Pitagorovim izrekom:
