Prijava z e-naslovom
Prijava brez gesla
Spomnimo se pravokotnega koordinatnega sistema v ravnini, v katerem vsako točko zapišemo z dvema podatkoma:
koordinato x in
koordinato y.
Tudi v polarnem kooridnatnem sistemu opisujemo točke v ravnini - s to razliko, da sta koordinati točke določene z:
oddaljenostjo točke od koordinatnega izhodišča in
s kotom med osjo x in pa daljico med koordinatnim izhodiščem in točko.
Kakšen koordinatni sistem izberemo za reševanje matematičnih problemov je povsem naša stvar - rezultat mora biti na koncu vedno enak. A pravilna izbira koordinat nam lahko v določenih primerih zelo olajša samo reševanje problema.
V primeru, da izberemo polarne kordinate, obenem izberemo polarni koordinatni sistem - ki se razlikuje od kartezičnega. Polarni koordinatni sistem v ravnini določata:
izhodišče O ali pol O;
pozitivni poltrak iz izhodišča p ali polarna os p.
Narišimo polarni koordinatni sistem:
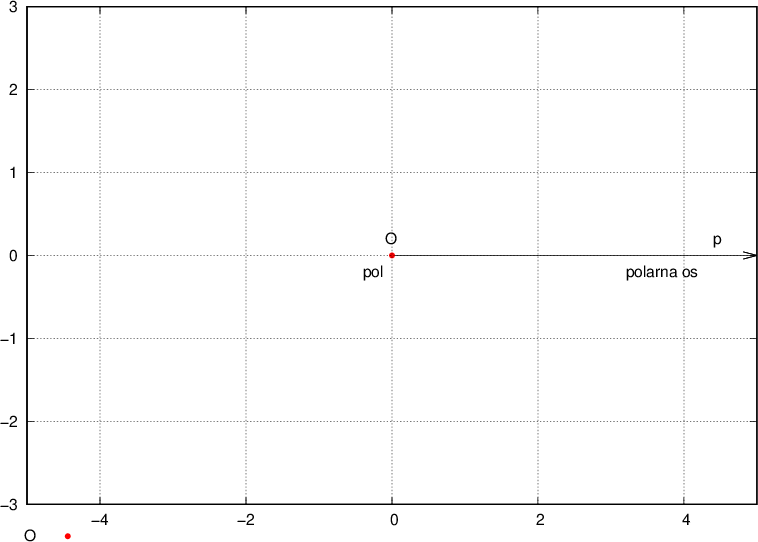
Lego točke, ki ni enaka izhodišču, določimo z dvema koordinatama:
z razdaljo r od pola O pa do dane točke in
s kotom φ, ki je kot med:
polarno osjo p in
daljice med točko in izhodiščem.
Kot φ vedno merimo v pozitivni smeri (nasprotna smer urinega kazalca) njegova vrednost pa je med 0°≤ φ <360°.
Koordinati φ in r imenujemo polarni koordinati točke in ju zapišemo kot urejen par:
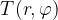
Pogosto je koordinata φ namesto v kotnih stopinjah podana v radianih. φ je tako omejen med 0 ≤ φ < 2π.
V nadaljevanju si bomo ogledali nekaj množic točk v polarnem koordinatnem sistemu. Te množice so zanimive zato, ker jih s polarnimi koordinatami precej enostavneje opišemo kot s kartezičnimi.
Krožnica je množica točk na ravnini, ki so enako oddaljene od izhodišča in sicer jo lahko opišemo s:
Kartezičnimi koordinatami
Krožnica je v pravokotnem koordinatnem sistemu (in s središčem v v izhodišču) podana z enačbo:
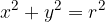
Polarnimi koordinatami
V polarnem koordinatnem sistemu je krožnica določena precej bolj ensotavno in sicer z enačbo:
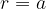
kjer je:
a številčna vrednost polmera krožnice (neko realno število);
φ pa zavzame vse možne vrednosti od 0° do 360°.
Poltrak je množica vseh takšnih točk v polarnem koordinatnem sistemu, ki:
poljuben r in
enak φ.
Kolobar je množica točk med dvema krožnicama. Povedano drugače: v kolobarju so točke omejene z najmanjšo in največjo dano razdaljo od izhodišča. Enačba kolobarja v polarnem koordinatnem sistemu je:
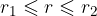
kjer sta:
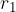najmanjša razdalja in
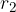največja dovoljena razdalja za oddaljenost od izhodišča.
V polarnem koordinatnem sistemu je krožni izsek množica točk, kjer:
prva koordinata, r, zavzame poljubne vrednosti od izhodišča O;
druga koordinata, φ, pa je omejena z dvema vrednostma:
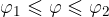
Izsek kolobarja je množica točk, kjer sta obe polarni koordinati omejeni.
