Osebne zbirke


Razumevanje koordinatnega sistema je osnova za vsakršno risanje grafov. Koordinatnih sistemov je lahko več, za nas pa bo v tem trenutku pomemben pravokotni koordinatni sistem.
Pravokotni koordinatni sistem imenujemo tudi kartezični koordinatni sistem. To ime je dobil po slavnemu matematiku Reneju Descartesu (1596-1650), ki je prvi zares izkoristil uporabnost takega koordinatnega sistema.
Pravokotni koordinatni sistem v ravnini sestavljata dve številski premici, ki se sekata v točki 0 (v izhodišču). Vodoravno premico imenujemo abscisna os, ki jo označimo z x in navpično ordinatna os, ki jo označimo z y.
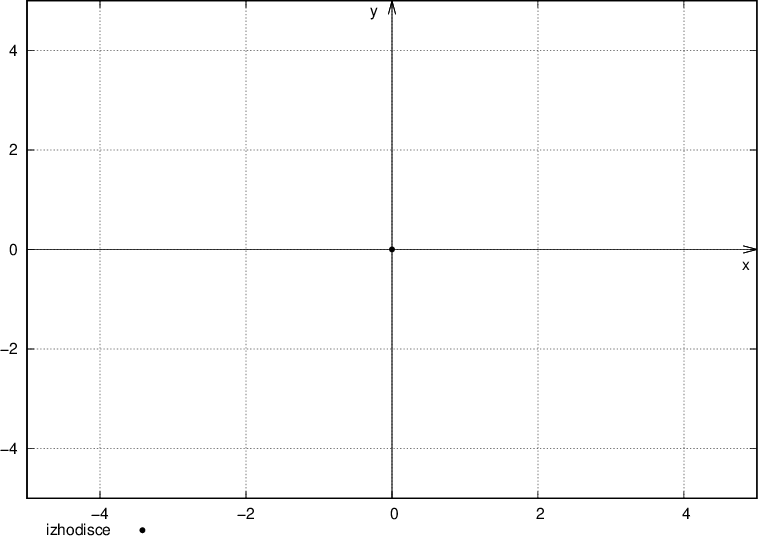
Točko, ki jo narišemo v koordinatni sistem, določata dve realni števili, ki ju imenujemo koordinatni točki T(x,y). Te dve števili nam povesta, kje v koordinatnem sistemu leži točka. Prva vrednost pripada abscisni osi in druga ordinatni osi.
Koordinatni sistem je razdeljen na štiri kvadrante:
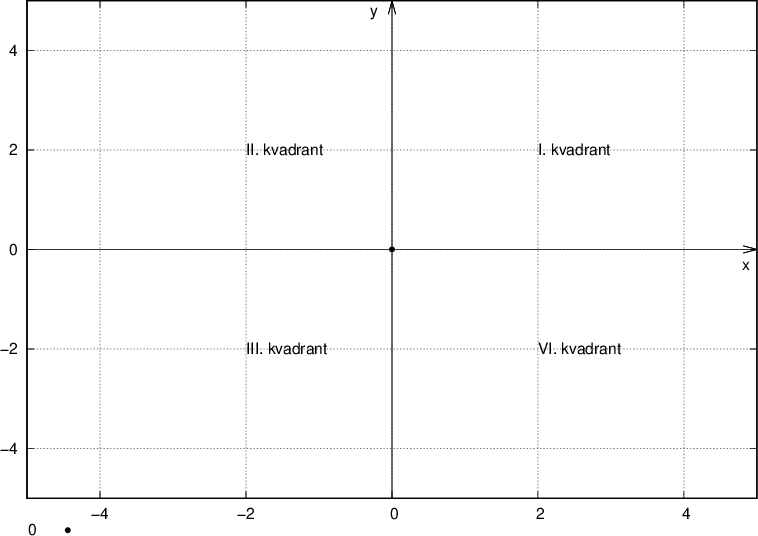
Iz grafa lahko razberemo, da:
imajo v prvem kvadrantu točke pozitivno absciso in ordinato
imajo v drugem kvadrantu točke negativno absciso in pozitivno ordinato
imajo v tretjem kvadrantu točke negativno absciso in negativno ordinato
imajo v četrtem kvadrantu točke pozitivno absciso in negativno ordinato
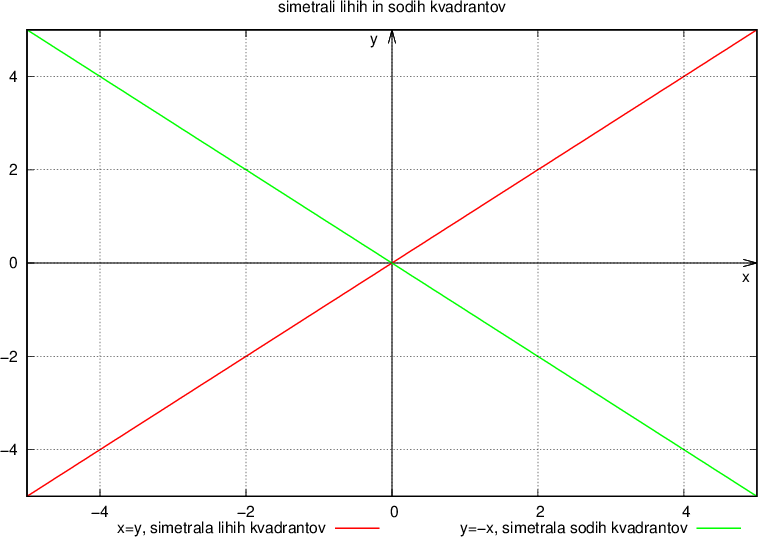
Poznamo dve simetrali kvadrantov:
simetralo lihih kvadrantov, ki jo določa linearna enačba y = x;
simetralo sodih kvadrantov, ki jo določa linearna enačba y = - x;
Zrcaljenje je skupno ime za več osnovnih geometrijskih preslikav. Vsako zrcaljenje ohranja razdalje med točkami, zato ga uvrščamo med toge premike. Ime zrcaljenje izhaja iz dejstva, da pri zrcaljenju dane geometrijske množice dobimo podoben rezultat kot pri odboju svetlobe na zrcalu.
Pri zrcaljenju vedno nastopata dva pojma:
točka ali množica točk ali funkcija, ki bo zrcaljena,
točka ali funkcija, prek katere se zrcali.
V nadaljevanju si bomo ogledali osnovna zrcaljenja. Zrcalili bomo točko prek koordinatnih osi oziroma prek koordinatnega izhodišča.
Točko v pravokotnem koordinatnem sistemu zrcalimo čez abscisno os tako, da narišemo zrcalno točko čez abscisno os. Ta pri tem ohranja lastnosti, ki jih ima točka, ki jo zrcalimo, torej je enako oddaljena od abscisne in ordinatne osi, le da se njen predznak pri ordinatni osi spremeni.
Zrcaljenje čez abscisno os zapišemo z:
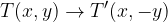
Točko v pravokotnem koordinatnem sistemu zrcalimo čez ordinatno os tako, da narišemo zrcalno točko čez ordinatno os. Ta pri tem ohranja lastnosti, ki jih ima točka, ki jo zrcalimo, torej je enako oddaljena od abscisne in ordinatne osi, le da se njen predznak pri abscisni osi spremeni.
Zrcaljenje čez ordinatno os zapišemo z:
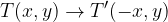
Točko v pravokotnem koordinatnem sistem zrcalimo čez koordinatno izhodišče tako, da narišemo zrcalno točko čez izhodišče. Ta pri tem ohranja lastnosti, ki jih ima točka, ki jo zrcalimo, torej je enako oddaljena od abscisne in ordinatne osi ter se njen predznak pri obeh koordinatah spremeni.
Zrcaljenje čez izhodišče zapišemo z:
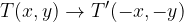
Zdaj, ko vemo kako narisati točko v pravokotni koordinatni sistemu, si bomo pogledali nekaj primerov kako narišemo množico točk v ravnini. Poglejmo si nekaj osnovnih primerov.