Osebne zbirke


O longitudinalnem ali vzdolžnem valovanju govorimo, ko delci snovi nihajo v isti smeri, kot se širi val. Longitudinalno valovanje povzroča nihalo, ki niha v smeri širjenja valovanja. Nihanje nihala se prenaša na prožni medij, ki se zaradi nihanja stiska in razteguje. V njem se pojavljajo zgoščine in razredčine, ki se širijo stran od izvora.
Pri longitudinalnem valovanju imamo največkrat v mislih širjenje zvoka v zraku. V tem primeru nihajo molekule zraka. Longitudinalni valovi pa se lahko širijo tudi v kapljevinah in trdnih snoveh, največkrat v kombinaciji s transverzalnim valovanjem.
Longitudinalno valovanje bomo v tem gradivu spoznali na primeru vijačne vzmeti.
Za nastanek longitudinalnih valov potrebujemo nihalo, ki niha v isti smeri, kot se širijo valovi. V stiku z nihalom je prožni medij (npr. vijačna vzmet, zrak, guma itd.) ki ga lahko nihalo razpenja in stiska. Nastajajo razredčine in zgoščine, ki se širijo stran od izvora s hitrostjo c.
Opazujmo nastanek longitudinalnega vala na vijačni vzmeti. V ta namen vzamemo brnač in ga povežemo z vijačno vzmetjo tako, da lahko niha v smeri vzmeti. Priključimo ga na izmenično napetost, kot kaže slika 3.
Kotev brnača je nihalo, ki harmonično niha od skrajno leve, do skrajno desne lege, kot kaže graf na sliki 4 zgoraj. Med nihanjem razpenja in stiska vzmet. Gostota kolobarjev se spreminja, na vzmeti nastajajo razredčine in zgoščine, odvisno, v katero smer se opazovani trenutek kotev premika. Razredčine in zgoščine nato potujejo vzdolž vzmeti.
Poglejmo malo podrobneje sliko 3:
Premik kotve brnača v levo pomeni, da se bodo obroči vzmeti razmaknili. Ob kotvi bo nastalo področje z majhno gostoto kolobarjev na vzmeti. Pravimo mu tudi razredčina - rumeno področje na slika 3 zgoraj.
Ko se kotva brnača premakne na desno, povzroči, da se navoji vzmeti stisnejo, povzroči veliko gostoto kolobarjev, zgoščino - rdeče področje na sliki 3 spodaj. Predhodna razredčina se bo medtem že premaknila vzdolž vzmeti na desno.
Nihanje kotve po sliki 3 je harmonično in ga opisuje enačba:

Pojasnimo, zakaj smo izbrali takšno funkcijo. Ker je nihalo (kotva) v začetku opazovanja v skrajni legi, smo smo izbrali funkcijo "kosinus". Kotva je na začetku skrajno levo in ima negativno amplituda odmika, zato je kosinus pomnožen še z negativno amplitudo 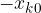 . Na grafu na sliki 4 vidimo, da imata nihanje kotve in gostote kolobarjev isto začetno obliko. Pravimo, da sta v fazi (oziroma sta sofazni).
. Na grafu na sliki 4 vidimo, da imata nihanje kotve in gostote kolobarjev isto začetno obliko. Pravimo, da sta v fazi (oziroma sta sofazni).
Predstavljajmo si, da fotografiramo valovaje na vzmeti v nekem trenutku 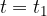 , ko je kotva brnača v skrajno levi legi - glej sliko 5. Poglejmo, kako se spreminja gostota kolobarjev, ko se na sliki pomikamo vzdolž vzmeti v desno.
, ko je kotva brnača v skrajno levi legi - glej sliko 5. Poglejmo, kako se spreminja gostota kolobarjev, ko se na sliki pomikamo vzdolž vzmeti v desno.
Na vzmet na sliki 5 smo označili nekatera področja:
razredčina A: Razredčina se pojavi ob brnaču, ko je kotva v skrajno levi legi in napenja vzmet. Ponavlja se vzdolž vzmeti na vsako valovno dolžino 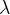 . Gostota obročev vzmeti je tam najmanjša.
. Gostota obročev vzmeti je tam najmanjša.
zgoščina C: Zgoščina je v našem primeru na polovici valovne dolžine od izvora in se ponavlja vsako valovno dolžino. Pravimo ji valovni hrbet. Gostota obročev vzmeti je tam največja.
nevtralna lega B: Med skrajnima legama kotve A in C je nevtralna ali ravnovesna lega B. Tam je gostota obročev takšna, kot bi bila v vzmeti, na kateri ni valovanja.
Zgoščine in razredčine se od izvora prenašajo naprej s pomočjo nihanja delcev vzmeti. Od amplitude tega nihanja je odvisna tudi energija, ki jo prenaša valovanje.
Narišimo vzmet najprej v ravnovesni legi, ko je njena oblika še nespremenjena - slika 4 A. Zatem narišimo še valujočo vzmet - slika 4 B. Opazovan trenutek je, ko je kotva brnača v skrajno levi legi in ustvarja na začetku vzmeti razredčino.
Poglejmo, kakšna je lega posameznih navojev glede na vzmet v ravnovesni legi. Za lažje opazovanje na sliki s krožcem označimo vsak četrti navoj:
razredčina - označena z modrim krožcem
nevtralna lega - označena z zelenim krožcem
zgoščina - označena z rdečim križcem
nevtralna lega - označena z zelenim krožcem
itd.
Vidimo, da ima največji odmik od ravnovesne lege del vzmeti, označen z zelenim krožcem. Tam je gostota kolobarjev enaka kot pri nedeformirani vzmeti (nevtralna lega). Na tem mestu je torej amplituda 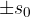 odmika. Odmik je nič, ko je na vzmeti zgoščina ali razredčina.
odmika. Odmik je nič, ko je na vzmeti zgoščina ali razredčina.
Združimo sedaj grafa gostote kolobarjev in odmika od ravnovesne lege s slike 5 in 6. Grafa sta na sliki 7. Izbran trenutek opazovanja je, ko je kotva brnača na skrajno levi strani.
Iz slike vidimo, da amplituda odmika od ravnovesne lege 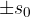 ko je ravnovesna gostota kolobarjev vzmeti in da je odmik nič v primeru zgoščine ali razredčine.
ko je ravnovesna gostota kolobarjev vzmeti in da je odmik nič v primeru zgoščine ali razredčine.
Kjer gre graf gostote kolobarjev skozi nič (vozel gostote), je hrbet odmika od ravnovesne lege. Ali obratno, kjer je vozel odmika 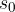 , je hrbet gostote - zgoščina ali razredčina.
, je hrbet gostote - zgoščina ali razredčina.
Zgoščine in razredčine se širijo od izvora vzdolž vzmeti s hitrostjo c. V času 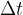 naredijo pot
naredijo pot 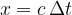 . V času enega nihaja
. V času enega nihaja 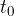 pa pot, ki je enaka valovni dolžini valovanja:
pa pot, ki je enaka valovni dolžini valovanja:
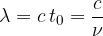
Upoštevali smo, da sta frekvenca in perioda recipročni:
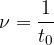
Pri določeni frekvenci bo valovna dolžina odvisna samo od hitrosti zvoka. Iz enačbe (1) izrazimo še frekvenco:
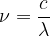
Odmik delcev od ravnovesne lege je odvisen je od opazovanega trenutka t in lege na vzmeti x. Označimo ga s funkcijskim zapisom s(x, t).
Opišimo najprej odmik s delcev le v odvisnosti od lege x na vzmeti, to je 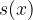 . Valovanje opazujemo v trenutku t = 0, ko je kotva skrajno desno.
. Valovanje opazujemo v trenutku t = 0, ko je kotva skrajno desno.
Funkcija, ki v času t = 0 opisuje odmik v odvisnosti od lege x, je:
V času 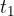 se val premakne vzdolž vzmeti za
se val premakne vzdolž vzmeti za 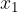 , kot kaže slika 6 zgoraj.
, kot kaže slika 6 zgoraj.
V zgoraj izpeljani enačbi upoštevajmo še ta premik oziroma časovni zamik.
Funkcija, ki opisuje odmik v odvisnosti od lege x in časa t, je:
Dobili smo enačbo, ki predstavlja odvisnost odmika delca (npr. vzmeti) od ravnovesne lege v odvisnosti od časa t in razdalje x. Narišimo graf - slika 7:
Potujoči harmonični longitudinalni val lahko zapišemo z enačbo: