Prijava z e-naslovom
Prijava brez gesla
Naravna števila 
ločimo v tri skupine glede na število deliteljev:
število 1, ki ima enega samega delitelja (samega sebe),
praštevila, ki imajo dva delitelja (1 in samega sebe),
sestavljena števila z več kot dvema deliteljema.
Praštevila lahko zapišemo v obliki produkta le na en način, kot zmnožek obeh deliteljev, števila 1 in samega sebe oziroma:
Praštevila so vsa tista naravna števila večja od 1, ki imajo v množici naravnih števil natanko dva delitelja; samega sebe in število 1.
Praštevil je neskončno mnogo.
Vrstni red faktorjev zaradi komutativnosti množenja ni pomemben.
Vsako sestavljeno število lahko zapišemo na več načinov kot produt svojih deliteljev. Vrstni red faktorjev v produktu zaradi komutativnosti množenja, kot smo že omenili, ni pomemben, faktorji, ki so večji od 1, pa se lahko večkrat ponovijo.
Sestavljena števila so vsa naravna števila večja od 1, ki niso praštevila. Vsa sestavljena števila imajo več kot dva delitelja.
Vsako naravno število lahko zapišemo kot produkt samih praštevil.
Osnovni izrek aritmetike
Vsako naravno število večje od 1 lahko na en sam način (če ne upoštevamo vrstnega reda faktorjev) zapišemo kot produkt potenc s praštevilskimi osnovami
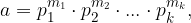
kjer so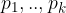 
praštevila in 
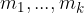naravna števila.
Praštevila 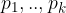imenujemo tudi prafaktorji števila 
.
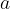Postopku iskanja prafaktorjev nekega števila pravimo razcep na prafaktorje oziroma prafaktorizacija.
Majhna števila lahko razcepimo na prafaktorje kar na pamet, za večja števila pa uporabimo postopek, ki je opisan v spodnjem primeru.
Lahko se zgodi, da pri razcepu naletimo na število, ki ga s pomočjo kriterijev deljivosti ne znamo razcepiti.
Na primer:
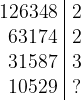
Večkrat se izkaže, da je tako število praštevilo. Poglejmo na primeru, kako to ugotovimo.
