Prijava z e-naslovom
Prijava brez gesla
Pri reševanju nalog z iskanjem presečišča dveh premic v koordinatnem sistemu so možne tri rešitve:
premici se sekata v presečišču, ki je točno določena točka
premici sta vzporedni in se ne sekata
premici sovpadata in je rešitev vsaka točka, ki leži na tej premici
Do rešitve lahko pridemo
grafično (v pravokotni koordinatni sistem narišemo premici in iz grafa preberemo rešitev);
računsko (reševanje sistema dveh enačb).
Koordinati presečišča sta takšna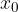 
in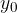 
, ki zadoščata obema enačbama, saj presečišče leži na obeh premicah. To pomeni, da za iskanje te točke rešimo s sistem dveh linearnih enačb z dvema neznakama.
Iskanje presečišča si bomo najlažje ogledali na konkretnih primerih.
Dve premici sta vzporedni natanko takrat, ko imata enaka smerna koeficienta. Če sta premici vzporedni se nikoli ne sekata in zato ne moremo izračunati presečišča. Sistem enačb tako nima rešitve.
Oglejmo si konkretni primer ko sta premici vzpredni.
Iz prejšnjih primerov smo videli, da imata dve premici lahko eno ali nobeno skupno točko. V zadnjem primeru pa si bomo videli, da imata premici lahko vse točke skupne. To je takrat ko sovpadata ali z drugimi besedami da sta identični.
Oglejmo si konkretni primer ko premici sovpadata.
