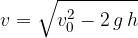Prijava z e-naslovom
Prijava brez gesla
Spustimo telo, da prosto pada. Predpostavimo, da pada v brezračnem prostoru in ga zato upor zraka med padanjem ne ovira. Gibanje tega telesa je enakomerno pospešeno. Pospešek pri padanju namesto z a označimo z g (od besede gravitacija - težnost). Pravimo mu težni pospešek, lahko tudi gravitacijski pospešek ali pa pospešek prostega pada.
Težni pospešek ni konstanta, pač pa se rahlo spreminja. Naštejmo nekaj dejavnikov, ki vplivajo na velikost (zemeljskega) težnega pospeška:
zemljepisno širino (na zemeljskih polih je nekoliko večji kot na ekvatorju);
nadmorsko višino (z višino pada);
sestavo tal (težke rudnine pod površjem rahlo povečajo g).
V naših računih bomo upoštevali, da je zemeljski težni pospešek enak:
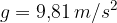
V vajah bomo, glede na natančnost ostalih podatkov, g zaokrožili na celo mesto (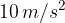
), na eno decimalno mesto 
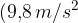) ali dve decimalni mesti.
Ker se telo pri prostem padu ali navpičnem metu giblje v navpični (vertikalni) smeri, bomo opravljeno pot označili z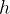 
(height = višina) namesto s 
.
Gravitacijski pospešek na površju Zemlje je enak za vsa telesa. Označimo ga z g. Takrat telo prosto pada s pospeškom g.
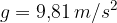
Veljo vse enačbe in vsi grafi, ki jih poznamo že iz poglavja Enakomerno pospešeno gibanje, le da namesto oznake a uporabimo oznako g in namesto s oznako h. Natančno izpeljavo formul najdete v poglavju Enakomerno pospešeno gibanje, tukaj jih le ponovimo.
Pri prostem padu ima telo v začetku hitrost 0 in mu nato narašča s težnim pospeškom g:
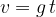
Graf spreminjanja hitrosti od časa t je:
Slika 1: prosti pad
Končna hitrost (slika 1), ob padcu na tla je:
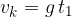
Višina, ki jo je telo preletelo med padanjem, je srednja hitrost krat čas oziroma velikost ploščine pod grafom hitrosti (površina obarvano v zeleno na sliki 1):
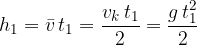
Čas, ko preleti višino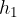 
je:
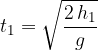
Končna hitrost, ko preleti višino 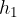pa je:
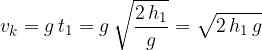
Ponovimo formule za prosti pad v splošni obliki - brez indeksov:
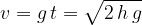
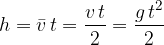
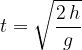
Telo vržemo navpično navdol. Pomeni, da smo mu dali začetno hitrost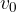 
, nato mu hitrost narašča zaradi gravitacijskega pospeška (glej sliko 2). Graf hitrosti, enačbe in izpeljave so enake kot pri enakomerno pospešenem gibanju z začetno hitrostjo 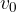, le namesto a pišemo g, pot pa namesto s s označimo s h.
Slika 2: prosti pad z začetno hitrostjo.
V trenutku, preden telo pade na tla, doseže končno hitrost:
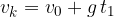
Višino padanja izračunamo tako, da množimo srednjo hitrost padanja s časom padanja:
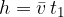
kjer je srednja hitrost:
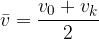
Opravljeno pot lahko izračunamo tudi kot ploščino pod grafom hitrosti:
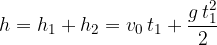
Končna hitrost v odvisnosti od višine, iz katere telo pade, pa je:
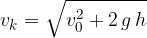
Pri metu navdzol z začetno hitrostjo 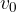veljajo naslednje formule v splošni obliki:
Hitrost padanja v odvisnosti od časa je:
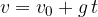
Višina padanja v odvisnosti od časa:
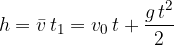
Hitrost padanja v odvisnosti od višine:
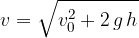
Telo vržemo navpično navzgor tako, da mu damo začetno hitrost 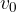. Hitrost telesu nato pada, saj na njega deluje gravitacijski pospešek, ki je nasprotno usmerjen od gibanja telesa. V nekem trenutku 
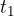se telo ustavi in hkrati doseže največjo višino 
.
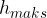Gibanje je enakomerno pojemajoče, kot smo ga spoznali v poglavju Enakomerno pospešeno gibanje, graf hitrosti v odvisnosti od časa pa je:
Slika 3: navpični met.
Grafi in enačbe, ki jih poznamo iz poglavja Enakomerno pojemajoče gibanje (natančneje, primer, ko ima telo začetno hitrost, ki s časom pada) ostanejo enake, zamenjamo le oznake: a z g in s s h.
Enačbe, ki opisujejo navpični met:
Hitrost v odvisnosti od časa je:
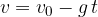
V trenutku :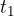
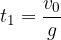
je njegova hitrost 0, telo pa je doseglo najvišjo višino. Višina telesa v odvisnosti od časa je:
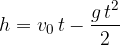
Maksimalna višina, ki jo doseže telo, je ploščina pod grafom hitrosti:
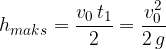
Začetna hitrost, potrebna da doseže določeno višino, je:
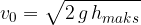
Hitrost telesa v odvisnosti od višine pa je:
