Osebne zbirke


Planet Zemlja nas privlači s silo, ki ji pravimo teža ali gravitacija. Če stojimo na tleh, čutimo težo, s katero delujemo na tla in s katero tla delujejo na nas. Kaj pa, če npr. skočimo iz letala? V tem primeru pa pod nogami nimamo tal, ki bi nas držala, zato se zaradi teže gibljemo. Temu gibanju, dokler je upor zraka zanemarljiv, pravimo prosti pad.
Kaj pa, če izletala istočasno skočita dva različno težka prijatelja? Bosta padala enako hitro? Zanima nas, če je hitrost padanja odvisna od mase. Naredimo preprost poskus.
Zaradi hitrosti pri padanju ni možno s prostimi očmi določiti, kakšno je to gibanje. Včasih so bile tudi meritve, s katerimi bi raziskali zakonitosti prostega pada, zelo težavne. Problem so bili nenatančni inštrumenti za merjenje kratkih časov. Posledično so mnogi verjeli, da je prosti pad enakomerno gibanje. Danes vemo, da je to enakomerno pospešeno gibanje s pospeškom, ki ga bomo določili v nadaljevanju.
V tem poglavju se bomo naučili, kako izračunati hitrost, pot in čas padanja telesa. Pri tem bomo zanemarili vpliv zračnega upora.
Danes je opazovanje padajočih teles teles precej lažje, kot v starejših časih. Na razpolago imamo hitre in natančne inštrumente za merjenje časa in hitrosti. Lahko si pomagamo tudi s fotografskim aparatom ali kamero. Tako lahko opazujemo prosti pad med počasnim predvajanjem posnetka.
Naredimo poskus s teniško žogico in izračunajmo njen pospešek pri prostem padu.
Dobljeni pospešek je pospešek prostega pada ali gravitacijski pospešek. Označimo ga z g. Natančnejša vrednost gravitacijskega pospeška je:
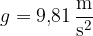
Zgornja vrednost pospeška prostega pada velja samo za padanje na površini planeta Zemlja. Natančne meritve bi pokazale, da se na različnih delih Zemlje ta pospešek celo malce razlikuje. Če se z vesoljskim plovilom dvignemo nad površino Zemlje, pa bo pospešek prostega pada manjši.
Vsako nebesno telo ima drugačen gravitacijski pospešek. Velja pa:
večja kot je masa nebesnega telesa, večji je njegov gravitacisjki pospešek,
bolj, kot se od nebesnega telesa oddaljimo, manjši je pospešek prostega pada.
Prosti pad je enakomerno pospešeno gibanje. Pospešek prostega pada je:
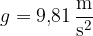
Zaokrožimo ga na:
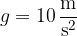
Prosti pad je torej enakomerno pospešeno gibanje z začetno hitrostjo nič. Predpostavili smo, da predmet le spustimo, da prosto pade. Če pa ga vržemo navzol, moramo upoštevati tudi začetnio hitrost.
Vse ugotovitve in enačbe, ki smo se jih naučili v poglavju Enakomerno pospešeno gibanje, veljajo tudi pri prostem padu, saj gre za isto gibanje. Spremenili bomo le nekatere oznake:
Namesto poti s bomo pisali višino h.
Namesto pospeška a bomo pisali gravitacijski pospešek g.
V nalogah bomo za gravitacijski pospešek vzeli približek:
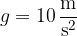
Pri izračunih si bomo pomagali z grafom hitrosti v odvisnosti od časa.
Hitrost enakomerno narašča s časom. Vsako sekundo naraste za 10 m/s. Trenutno hitrost izračunamo po enačbi:
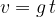
Predmet pade na tla v času 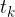 . Tik, preden pade na tla je njegova hitrost največja. Pravimo ji končna hitrost in ji damo oznako
. Tik, preden pade na tla je njegova hitrost največja. Pravimo ji končna hitrost in ji damo oznako 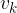 :
:
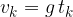
V poglavju Enakomerno pospešeno gibanje smo se naučili, da je pot (globina padanja h) enaka ploščini lika pod grafom hitrosti. V našem primeru je to zasenčen del zgornjega grafa v(t). Lahko pa jo izračunamo tudi z znano povprečno hitrostjo padanja.
Globino padanja izračunamo s pomočjo povprečne hitrosti
Globina padanja je povprečna hitrost padanja krat čas padanja:
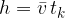
Pri tem je povprečna hitrost:
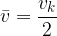
Izračun globine padanja s ploščino lika pod grafom hitrosti
Globina padanja je ploščina trikotnika:
Enačbo lahko na splošno zapišemo tudi brez indeksa k:
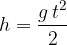
Iz podane višine, lahko izračunamo čas padanja. Izhajamo iz enačbe za pot (globino):
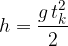
Izrazimo čas padanja:
S pomočjo dobljene enačbe bi lahko izračunali tudi končno hitrost pri podani globini padanja:
Poglejmo si primer, kjer iz podane višine izračunamo čas padanja.
Hitrost padanja pri podanem času padanja izračunamo po enačbi:
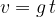
Hitrost padanja pri podani globini padanja izračunamo po enačbi:
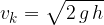
Globina padanja pri podanem času padanja je:
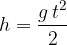
Čas padanja pri podani višini padanja je: