Osebne zbirke


V poglavju Verjetnost dogodka smo spoznali lastnosti verjetnosti, t.i. aksiome verjetnosti in aksiome Kolgomorova. V tem poglavju bomo spoznali še nekaj novih lastnosti in hkrati nekaj takih, ki jih že poznamo. Tokrat bomo njihove trditve tudi dokazali.
Uporaba teh dokazanih trditev nam lahko opazno olajša računanje verjetnosti dogodkov in nudi hitrejši način reševanja vaj, ki smo jih, pred vpeljavo trditev, reševali na daljši način.
Vemo, da se nemogoči dogodek - dogodek označim s črko N - nikoli ne more zgoditi. Očitno je torej, da je verjetnost takega dogodka enaka 0.
Verjetnost nemogočega dogodka N je enako 0:
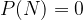
Dokaz
Naj bosta dogodka A in N nezdružljiva. Tedaj lahko z upoštevanjem aksioma verjetnosti zapišemo:
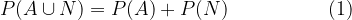
Ker očitno pa se dogodek N ne more zgoditi, lahko obenem zapišemo tudi:
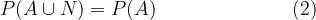
Dobljeni trditvi (1) in (2) izenačimo in dobimo:
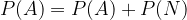
Iz česar očitno izhaja:
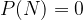
Verjetnost dogodku A nasprotnega dogodka A' je enaka 1 - verjetnost dogodka A.
Verjetnost nasprotnega dogodka (A') dobimo tako, da od 1 odštejemo verjetnost osnovnega dogodka (A):
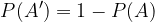
Dokaz
Definicija nasprotnega dogodka A' pravi, da sta z osnovnim dogodkom A nezdružljiva. Zato veljata trditvi:
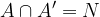
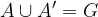
kjer je N nemogoči dogodek, G pa gotov dogodek. Po aksiomih verjetnosti lahko zato zapišemo:
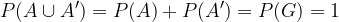
Kar je v resnici enako:
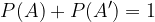
Oziroma:
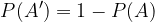
Verjetnost dogodka, ki je način nekega drugega dogodka , je vedno manjša ali enaka od verjetnosti tega drugega dogodka.
Če je dogodek A način dogodka B; se pravi 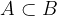 , potem velja:
, potem velja:
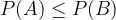
Dokaz
Če velja 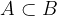 , potem lahko dogodek B zapišemo kot vsoto dveh nezdružljivih dogodkov: A in B – A. Njegova verjetnost je tako enaka:
, potem lahko dogodek B zapišemo kot vsoto dveh nezdružljivih dogodkov: A in B – A. Njegova verjetnost je tako enaka:
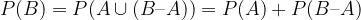
Oziroma okrajšano:
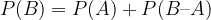
Za poljuben dogodek velja, da je njegova verjetnost nenegativno število: 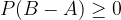 , zato očitno mora veljati neenakost:
, zato očitno mora veljati neenakost:
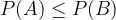
Verjetnost razlike dveh poljubnih dogodkov A in B je enaka razliki verjetnosti enega izmed dogodkov in verjetnosti preseka obeh dogodkov.
Verjetnost razlike dveh poljubnih dogodkov A in B zapišemo kot:
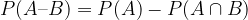
Dokaz
Dogodek A zapišemo kot vsoto dveh nezdružljivih dogodkov, dogodka 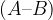 in
in 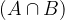 :
:
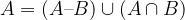
Z uporabo aksioma za računanje verjetnosti nezdružljivih dogodkov dobimo naslednjo zvezo:
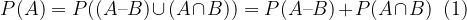
Dobljeno trditev (1) preuredimo in dobimo:
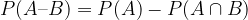
Kako izračunamo verjetnost vsote dveh poljubnih dogodkov, ko npr. dogodka nista nezdružljiva?
Verjetnost vsote dveh poljubnih dogodkov A in B zapišemo kot:
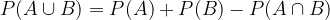
Dokaz
Naj bosta dogodka A in B poljubna. Velja, da sta dogodka A - B in B nezdružljiva, njuna vsota pa je enaka vsoti dogodkov A in B: 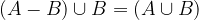 . Z upoštevanjem aksioma verjetnosti dveh nezdružljivih dogodkov lahko zapišemo:
. Z upoštevanjem aksioma verjetnosti dveh nezdružljivih dogodkov lahko zapišemo:
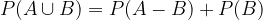
Z upoštevanjem trditve o razliki odgodkov, lahko dobljeno verjetnost 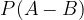 zapišemo z
zapišemo z 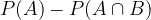 . Dobimo:
. Dobimo:
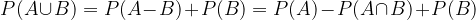
Preuredimo in dobimo:
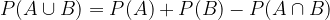
Vrednost verjetnosti poljubnega dogodka ne more biti nikoli večja od 1.
Verjetnost poljubnega dogodka ne more nikoli preseči 1:
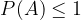
Dokaz
Za vsak dogodek velja, da je način gotovega dogodka: 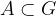 . Hkrati vemo, da za gotovi dogodek velja:
. Hkrati vemo, da za gotovi dogodek velja: 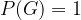 . Zato lahko, z upoštevanjem aksiomov verjetnosti in zgoraj dokazane relacije med dogodkom, ki je način drugega dogodka, sklepamo, da velja:
. Zato lahko, z upoštevanjem aksiomov verjetnosti in zgoraj dokazane relacije med dogodkom, ki je način drugega dogodka, sklepamo, da velja:
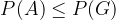
In: