Verjetnostni račun

Verjetnostni račun je del matematike, ki preučuje kakšna je verjetnost, da se zgodi nek naključni dogodek.

Vsako opazovanje, izvajanje ali merjenje nekega pojava imenujemo poskus. Poskus so torej dejavnosti, ki se vedno zgodijo v istem zaporedju

Dogodek je vsak rezultat, ki ga dobimo ob izvajanju poskusa.

Met kovanca vedno opravimo na enak način. Vzamemo kovanec v roko in vržemo. Temu zaporedju dejavnosti sledi, da se bo kovanec obrnil na eno izmed dveh strani in sicer ali cifra ali grb. Na katero stran se bo obrnil je odvisno od slučaja, zato bomo to imenovali slučajni dogodek.

Nekateri dogodki se zgodijo ob vsaki ponovitvi poskusa. Za nočjo pride dan, za petkom pride sobota, ob metu kocke bo padlo število od 1 do 6 in podobno. Takim dogodkom pravimo gotovi dogodki, ker se zgodijo z gotovostjo ob vsaki ponovitvi poskusa. Predvidevamo, da bi se zgodili vedno, tudi če bi poskus ponavljali v nedogled.

Druga skrajnost so nemogoči dogodki, dogodki, ki se ne zgodijo nikoli, ne glede na to kako dolgo ponavljamo poskus. Primer nemogočega dogodka je, da bi ob metu navadne kocke dobili število 7.

Slučajne dogodke bomo označevali z velikimi črkami A,B,C,..., gotov dogodek bo imel oznako G, nemogoč dogodek pa N. Poskus bomo označevali s črko X.

Vsi dogodki 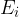pri metu kocke so takšni, da se jih ne da zapisani kot vsoto ali produkt nekih drugih dogodkov. Torej so osnovni ali elementarni dogodki. Iz elementarnih dogodkov z operatorji tvorimo sestavljene dogodke.

Množico vseh elementarnih dogodkov imenujemo vzorčni prostor poskusa. Mi se bomo omejili le na končne vzorčne prostore. Vsota vseh elementarnih dogodkov je gotov dogodek, dva po dva elementarna dogodka pa sta nezdružljiva.

Če je vzorčni prostor sestavljen iz N dogodkov, lahko gotovi dogodek zapišemo kot:

Nemogoči dogodek pa zapišemo kot:

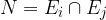
kjer velja:

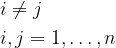
Vzorčni prostor upodobimo kot kvadrat, elementarne dogodke pa kot pike v njem.

Iz teorije množic se spomnimo, da ima množica z n elementi 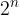podmnožic. Analogno lahko vidimo, da lahko iz vzorčnega prostora z n elementarnimi dogodki sestavimo 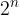različnih vsot dogodkov. Med temi dogodki lahko na več načinov izberemo tiste, ki so paroma nezdružljivi njihova vsota pa predstavlja gotov dogodek. Taki dogodki sestavljajo popoln sistem dogodkov poskusa X.

Z dogodki računamo podobno kot z množicami in uporabljamo enake operatorje. Tudi grafično dogodke upodabljamo z Vennovimi diagrami.

Vsoto dogodkov A in B označimo z 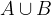. Ta dogodek se zgodi, ko se zgodi ali A ali B, torej vsaj eden izmed dogodkov.

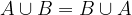
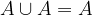
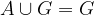
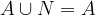
Produkt dogodkov 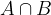se zgodi, ko se zgodita A in B hkrati. Če se dogodka A in B ne moreta zgoditi hkrati ju imenujemo nezdružljiv dogodek, njun produkt pa je nemogoč dogodek. Če produkt ni nemogoč dogodek pa sta A in B združljiva dogodka.

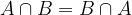
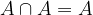
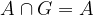
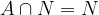
Nasprotni dogodek A' dogodka A se zgodi, če se A ne zgodi.

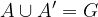
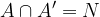
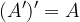
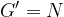
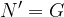
Razlika dogodkov 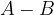se zgodi, če se zgodi dogodek A in se hkrati ne zgodi dogodek B.

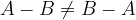
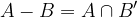
Dogodek A je način dogodka B, označimo 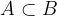, če se vsakokrat, ko se zgodi A, hkrati zgodi tudi B.