Osebne zbirke


Množice smo že spoznali v gradivu Množice. V tem gradivu pa si poglejmo operacije med njimi.
Unija dveh množic je množica, ki vsebuje vse elemente prve in vse elemente druge množice.
Unijo množic A in B označimo kot:
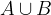
in vsebuje vse elemente iz obeh množic.
Presek dveh množic je množica, ki vsebuje vse elemente, ki so hkrati v prvi in v drugi množici.
Presek množic A in B označimo kot:
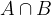
in vsebuje elemente, ki so v obeh množicah.
Množici, ki imata prazen presek (torej 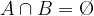 ), pravimo da sta tuji ali disjunktni množici.
), pravimo da sta tuji ali disjunktni množici.
Razlika dveh množic je množica, ki vsebuje vse elemente iz prve množice, ki niso hkrati v drugi množici.
Razliko množic A in B označimo kot:

ali
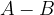
in vsebuje elemente iz množice A, ki niso v množici B.
Komplement množice je množica, ki vsebuje tiste elemente univerzalne množice, ki niso vsebovani v množici.
Komplement množice A označimo kot:
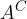
in vsebuje elemente iz množice U (univerzalne množice), ki niso v množici A.
Kartezični produkt množic je množica vseh mogočih urejenih parov, pri čemer je prvi element urejenega para iz prve množice, drugi pa iz druge.
Kartezični produkt A in B označimo kot:
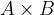
in vsebuje urejene pare.