Osebne zbirke


Ravninski kot je del ravnine, ki ga omejujeta dva poltraka z istim izhodiščem. Poltraka imenujemo kraka kota, njuno skupno izhodišče pa vrh kota. Vrh kota označimo z veliko tiskano črko V, celoten kot pa označimo z malo črko grške abecede (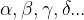 ).
).
Če na vsakem poltraku označimo po eno točko, lahko kot označimo tudi kot 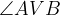 :
:
Pri slednjem označevanju upoštevamo vedno konveksni kot.
Najpogosteje kote merimo v kotnih stopinjah in v radianih.
Oznaka za kotno stopinjo je °. Polni kot meri 360°. Kotne stopinje lahko razdelimo na še manjše enote. Kotna minuta znaša 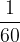 kotne stopinje, kotna sekunda pa
kotne stopinje, kotna sekunda pa 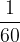 kotne minute. Za eno kotno stopinjo tako potrebujemo 3600 kotnih sekund.
kotne minute. Za eno kotno stopinjo tako potrebujemo 3600 kotnih sekund.
Oznaka za radian je rad. Polni kot meri 2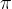 . Radian je enota brez razsežnosti, zato je običajno ne pišemo.
. Radian je enota brez razsežnosti, zato je običajno ne pišemo.
V geometriji posebno pozornost namenjamo naslednjim kotom:
kot nič meri 0° oz. 0 rad (radianov). Poltraka, ki ga omejujeta, se pri kotu nič prekrivata:
pravi kot meri 90° oz. 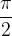 rad. Poltraka, ki ga omejujeta, sta pravokotna eden na drugega:
rad. Poltraka, ki ga omejujeta, sta pravokotna eden na drugega:
iztegnjeni kot meri 180° oz. 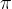 rad. Poltraka, ki ga omejujeta, sestavljata premico:
rad. Poltraka, ki ga omejujeta, sestavljata premico:
polni kot meri 360° oz. 2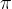 rad. Poltraka, ki ga omejujeta, se znova prekrivata:
rad. Poltraka, ki ga omejujeta, se znova prekrivata:
Če kotu prištejemo ali odštejemo večkratnik polnega kota, dobimo nazaj znova prvotno orientacijo v ravnini. Zato uporabljamo vrednosti kotov med 0 in 360 stopinjami. Več o tem bo govora v poglavju o trigonometriji.
Kote lahko razvrstimo v naslednje skupine:
Ostri koti so vsi koti med kotom nič in pravim kotom:
Topi koti so vsi koti med pravim kotom in iztegnjenim kotom:
Izbočeni koti so vsi koti med kotom nič in iztegnjenim kotom:
Vdrti koti so vsi koti med iztegnjenim kotom in polnim kotom:
Najbolj značilne relacije dvojic kotov so naslednje:
Komplementarna kota merita skupaj 90°:
Suplementarna kota merita skupaj 180°:
Sosednja kota imata skupen vrh in en krak:
Sosednja kota skupaj tvorita nov kot, ki je enak njuni vsoti.
Sovršna kota imata skupen vrh, njuni kraki pa oblikujejo dve premici, ki se sekata:
Sovršna kota sta enake velikosti. Rečemo tudi, da sta skladna.
Izmenična kota si delita en krak, druga dva kraka pa sta vzporedna in obrnjena v nasprotne smeri:
Tudi izmenična kota sta skladna.
Pri razlagi se omejimo na konveksne kote.
Kota z vzporednimi kraki sta:
skladna, če sta oba kraka vzporedna v isto smer
skladna, če sta oba kraka vzporedna v nasprotno smer
suplementarna, če je en krak vzporeden v isto smer, drug pa v nasprotno smer
Kota s pravokotnimi kraki sta:
suplementarna, če leži vrh enega kota v notranjosti drugega. V tem primeru je en kot oster, drugi pa top.
skladna, če leži vrh enega kota zunaj drugega. V tem primeru sta oba kota ostra.