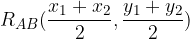Osebne zbirke


V pravokotnem koordinatnem sistemu sta dani dve točki 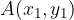 in
in 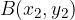 . Izračunati želimo razdaljo med njima oz. dolžino daljice
. Izračunati želimo razdaljo med njima oz. dolžino daljice 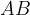 .
.
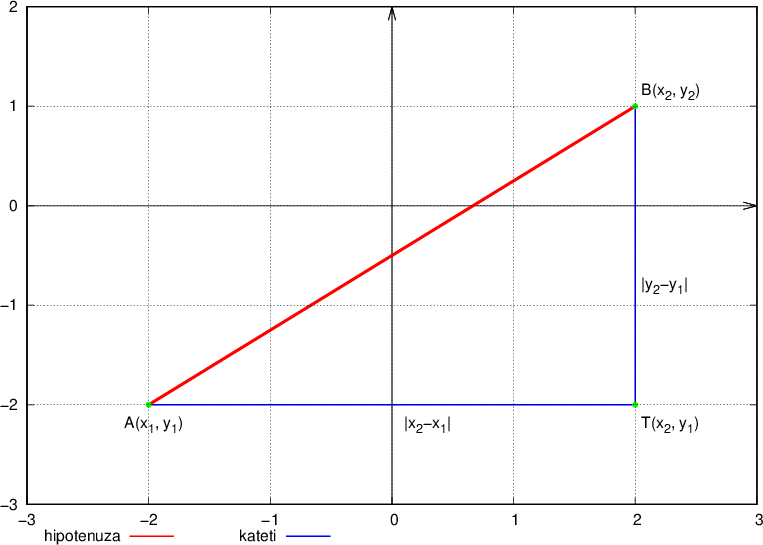
S skice opazimo, da imamo opravka s pravokotnim trikotnikom, kar pomeni, da lahko uporabimo Pitagorov izrek:
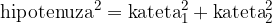
Razdalja med dvema točkama je vedno nenegativno število, zato pri dolžini katet pravokotnega trikotnika uporabimo absolutno vrednost. Zapišimo obe kateti:
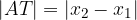
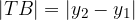
Pitagorov izrek za izračun hipotenuze oz. dolžine 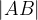 se glasi:
se glasi:
Enačba za razdaljo med dvema točkama je:
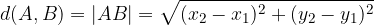
Oznaka za razdaljo d je prva črka latinske besede distancia, ki pomeni razdalja.
Razdalja med poljubnima točkama je vedno nenegativno število:
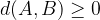
Razdalja med dvema točkama je enaka 0 natanko takrat, ko točki sovpadata:
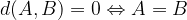
Razdalja od točke A do točke B je enaka razdalji od točke B do točke A:
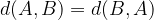
Razdalja od A do C je manjša ali enaka vsoti razdalj od A do B in od B do C:
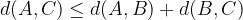
Aritmetična sredina dveh vrednosti x in y je enaka 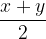 .
.
Razpolovišče daljice s krajiščema 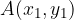 in
in 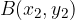 je točka:
je točka: