Osebne zbirke


Razmerje nam pove velikostni odnos med količinami. Pogosto se srečujemo z razmerjem med dvema količinama, ki ga zapišemo v obliki:
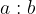
in beremo: a proti b.
Kadar razmerja med seboj enačimo, govorimo o sorazmerju.
Sorazmerje v katerem med seboj enačimo dve količini, zapišemo kot:
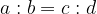
pri čemer 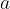 in
in 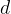 imenujemo zunanja člena,
imenujemo zunanja člena, 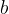 in
in 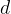 pa notranja.
pa notranja.
Ker razmerje v matematiki predstavlja deljenje, ga lahko zapišemo tudi kot ulomek:
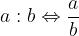
Potem sorazmerje v matematiki predstavlja enačba z ulomki:
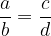
Pri računanju sorazmerij upoštevamo pravila za računanje z ulomki.
Glede na odnose med količinami, ločimo dva tipa sorazmerij:
prema sorazmerja in
obratna sorazmerja
Kadar se s povečanjem ene količine poveča tudi druga količina, govorimo o premem sorazmerju.
Premo sorazmerje zapišemo:
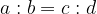
pri čemer 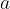 in
in 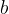 označujeta prvo količino
označujeta prvo količino  in
in 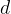 pa drugo. Če količini križno zmnožimo (glej podpoglavje v nadaljevanju), premo sorazmerje lahko zapišemo tudi kot:
pa drugo. Če količini križno zmnožimo (glej podpoglavje v nadaljevanju), premo sorazmerje lahko zapišemo tudi kot:
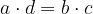
Križni račun navadno uporabimo, ko imamo opravka s premim sorazmerjem. V križnem računu nastopajo štiri števila, naj bodo to a, b, c, d, za katera velja:
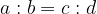
Izraz preoblikujemo v ulomka:
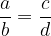
S križnim računom ulomek pretvorimo v zmnožek in sicer velja, da mora biti zmnožek diagonal enak:
S križnim računom izraz:
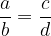
pretvorimo v zmnožek (množimo po diagonali):
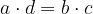
Kadar se s povečanjem ene količine druga količina zmanjša, govorimo o obratnem sorazmerju.
Obratno sorazmerje zapišemo kot:
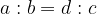
pri čemer 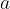 in
in 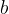 označujeta prvo količino
označujeta prvo količino  in
in 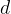 pa drugo. Količini sta obratnosorazmerni, če velja:
pa drugo. Količini sta obratnosorazmerni, če velja:
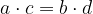
Kadar med seboj enačimo več kot dve količini, govorimo o sestavljenem sorazmerju.
Sestavljeno sorazmerje zapišemo kot:
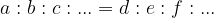
Če želimo, da zgornja enačba velja, morajo biti količniki istoležnih členov sorazmerja med seboj enaki. Skupni količnik označimo s k:
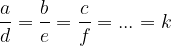
Ob upoštevanju zgornje enačbe za sorazmerje lahko zapišemo:
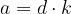
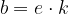
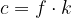

in sestavljeno sorazmerje prepišemo v:
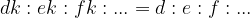
Sestavljeno sorazmerje lahko zapišemo tudi v naslednji obliki:
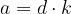
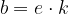
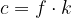

pri čemer k predstavlja koeficient sorazmerja.
Poseben primer sestavljenega sorazmerja so zaporedno sestavljena sorazmerja, kjer imamo sicer opraviti z več količinami, ki pa med seboj niso neposredno povezana, ampak imamo eno neznano količino, za katero najprej pogledamo v kakšnem sorazmerju je z ostalimi količinami in za vsako količino posebej določimo sorazmerje. Nato zapišemo zaporedno sorazmerje.
Zaporedno sestavljeno sorazmerje zapišemo kot:
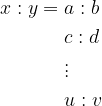
pri čemer je x ali y neznana količina, za katero pogledamo v kakšnem sorazmerju je z ostalimi količinami.
Zaporedno sorazmerje nadomestimo z enostavnim:
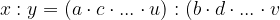
in ga rešimo kot je to opisano v podpoglavju sorazmerja.