Osebne zbirke


Snovi v vseh treh fazah (trdno, tekoče, plinasto) s temperaturo spreminjajo svoj volumen. Pojavu pravimo temperaturno raztezanje.
S tem pojavom smo se že srečali v poglavju Plinska enačba. Spoznali smo odvisnost volumna plina od temperature pri konstantnem tlaku. Omenjena odvisnost je Gay-Lussacov zakon. Plin se pri konstantnem tlaku s temperaturo razpenja - veča se mu volumen. Spremembo volumna s temperaturo lahko za idealni plin tudi natančno izračunamo s pomočjo plinske enačbe:
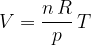
Sprememba volumna s temperaturo pa je:
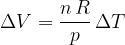
Enačbi med seboj delimo:
Faktor 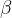 poimenujemo volumenski temperaturni koeficient idealnega plina. Pri idealnih plinih je strogo določen z recipročno vrednostjo absolutne temperature pred opazovano spremembo.
poimenujemo volumenski temperaturni koeficient idealnega plina. Pri idealnih plinih je strogo določen z recipročno vrednostjo absolutne temperature pred opazovano spremembo.
Podobno kot za plin velja enačba tudi za večino kapljevin. Molekule zaradi temperature med sabo trkajo in se odrivajo. Tudi pri večini trdnih snovi velja podobno. Zaradi termičnega nihanja zavzemajo molekule več prostora, skupni volumen se veča.
Obstajajo pa tudi izjeme, ko se volumen snovi s temperaturo manjša. Pravimo, da imajo negativni temperaturni razteznostni koeficient.
Vzemimo palici dolžine a in jo segrejemo za 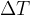 . Palica se bo podaljšala za
. Palica se bo podaljšala za 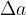 , kot kaže slika.
, kot kaže slika.
Količnik med podaljškom in prvotno dolžino imenujemo relativni podatljšek. Relativni podaljšek je sorazmeren spremembi temperature:
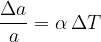
oziroma

Faktor 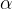 imenujemo linearni temperaturni razteznostni koeficient.
imenujemo linearni temperaturni razteznostni koeficient.
Dolžina palice po temperaturnem raztezanju je:
Relativni linearni podaljšek je sorazmeren s spremembo temperature:
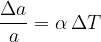
kjer je 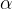 linearni razteznostni koeficient. Posledično je dolžina segrete palice:
linearni razteznostni koeficient. Posledično je dolžina segrete palice:
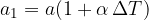
Tabela koeficientov dolžinskega raztezka za nekatere materiale.
Vzemimo kvader s stranicamo a, b in c. Ko kvader segrevamo, se podaljšajo stranice za 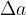 ,
, 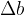 in
in 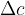 kot kaže slika. S tem se poveča tudi prostornina.
kot kaže slika. S tem se poveča tudi prostornina.
S slike razberemo približen izraz, za koliko se je povečal volumen:
Pri izračunu se zavedamo, da smo zanemarili majhne kvadre ob robovih s skupnim volumnom:
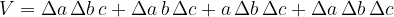
Prostornina po temperaturnem raztezanju je sedaj:
Relativno povečanje volumna telesa je sorazmerno spremembi temperature:
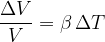
kjer je 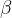 volumenski razteznostni koeficient. Približno velja, da je:
volumenski razteznostni koeficient. Približno velja, da je:
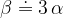
Volumen snovi po segrevanju lahko zapišemo z enačbo:
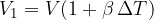
Tabela koeficientov prostorninskega raztezka za nekatere materiale: