Osebne zbirke


Trikotnik je geometrijski lik s tremi oglišči in s tremi stranicami.
Oglišča označujemo z velikimi tiskanimi črkami 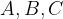 , stranice pa z malimi tiskanimi črkami
, stranice pa z malimi tiskanimi črkami 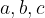 :
:
Oglišča trikotnika so nekolinearne točke, za stranice trikotnika pa velja trikotniška neenakost:
Vsota dolžin katerihkoli dveh stranic trikotnika je večja od dolžine tretje stranice:
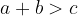
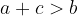
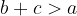
V pozitivno usmerjenem trikotniku si oglišča v zaporedju 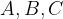 sledijo v smeri nasprotno od smeri urinega kazalca:
sledijo v smeri nasprotno od smeri urinega kazalca:
V negativno usmerjenem trikotniku si oglišča v zaporedju 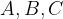 sledijo v smeri urinega kazalca:
sledijo v smeri urinega kazalca:
Matematično pozitivna smer in smer vrtenja urinih kazalcev sta si nasprotni.
Poleg obravnavane usmerjenosti trikotnika se z omenjenim pojavom srečamo tudi pri kotih.
Višina trikotnika je razdalja med ogliščem in nosilko nasprotne stranice.
Višina trikotnika je daljica, katere nosilka je tista pravokotnica na stranico, ki poteka skozi nasprotno oglišče.
Trikotnik ima tri višine. Označujemo jih s 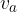 ,
, 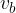 in
in 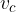 .
.
Presečišče nosilk višin imenujemo višinska točka in jo označimo z 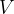 :
:
Težiščnica trikotnika je daljica s krajišči:
na oglišču in
na razpolovišču nasprotne stranice.
Trikotnik ima tri težiščnice. Označujemo jih s 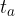 ,
, 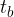 in
in 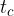 .
.
Nosilke težiščnic se sekajo v točki, ki jo imenujemo težišče. Označimo ga s 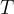 :
:
Srednjica je daljica, ki je vzporedna eni od stranic in povezuje središči ostalih dveh stranic trikotnika.
Dolžina srednjice je enaka polovični vrednosti stranice, kateri je vzporedna:
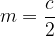
Običajno se srednjico označuje z malo črko s, da pa je ne bomo zamenjevali s polovičnim obsegom trikotnika, ki se prav tako označi z malo črko s, smo si zanjo izbrali oznako m.
Notranji kot je konveksni kot z vrhom v oglišču trikotnika, njegova kraka pa potekata skozi preostali dve oglišči. Notranje kote trikotnika označujemo z malimi grškimi črkami 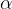 ,
, 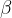 in
in 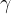 :
:
Vsota notranjih kotov trikotnika je 180° (iztegnjeni kot).
Zunanji kot je sokot pripadajočega notranjega kota. Zunanji koti so konveksni. Zunanje kote trikotnika označujemo z malimi grškimi črkami, ki jim dodamo opuščaj - apostrof (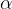 ' ,
' , 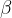 ' in
' in 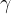 '):
'):
Vsota zunanjih kotov trikotnika je 360° (polni kot).
Zunanji kot trikotnika je enak vsoti obeh nasprotnih notranjih (nepriležnih) kotov:
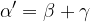
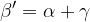
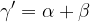
Nahaja se v sečišču simetral vseh treh stranic. Označimo ga z 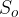 . Na krožnici očrtanega kroga ležijo vsa tri oglišča:
. Na krožnici očrtanega kroga ležijo vsa tri oglišča:
Podrobno razlago najdete v poglavju o krogu in krožnici.
Nahaja se v sečišču simetral vseh treh kotov. Označimo ga z 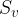 . Krožnica včrtanega kroga se dotika vseh treh stranic, a jih ne seka:
. Krožnica včrtanega kroga se dotika vseh treh stranic, a jih ne seka:
Podrobno razlago najdete v poglavju o krogu in krožnici.
Zanj je značilno, da ima enako dolge stranice in skladne notranje kote (vsak notranji kot meri 60°):
Enakostranični trikotnik je pravilni trikotnik, ker so vse njegove stranice enako dolge in vsi njegovi koti med seboj skladni.
V njem je en notranji kot pravi (znaša 90°). Stranica nasproti pravega kota je najdaljša in jo imenujemo hipotenuza, ostali dve stranici pa sta kateti. V pravokotnem trikotniku veljajo kotne funkcije.
Zanj je značilno, da ima dve stranici enako dolgi (imenujemo ju tudi kraka trikotnika), skladna pa sta tudi dva notranja kota. Tretjo stranico imenujemo osnovnica:
Če enakokraki trikotnik z višino na osnovnico 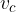 razdelimo na pol, dobimo dva skladna pravokotna trikotnika:
razdelimo na pol, dobimo dva skladna pravokotna trikotnika:
Splošno se obseg trikotnika izračuna na naslednji način:
Obseg splošnega trikotnika:
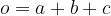
Obseg za posebne primere trikotnika se glasi:
Obseg enakokrakega trikotnika:
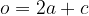
Obseg enakostraničnega trikotnika:
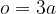
Splošno se ploščina trikotnika pri podani stranici in višini na to stranico izračuna na naslednji način:
Splošna formula za izračun ploščine trikotnika:
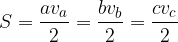
Če imamo podane vse 3 stranice, ploščino računamo po naslednji enačbi:
Heronov obrazec za izračun ploščine trikotnika:
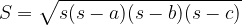
pri čemer je s polovični obseg trikotnika:
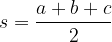
Če imamo podan polmer trikotniku včrtanega ali očrtanega kroga, ploščino lahko izračunamo po naslednjih enačbah:
Ploščina trikotnika, izražena s polmerom r trikotniku včrtanega kroga:
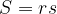
pri čemer je s polovični obseg trikotnika:
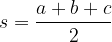
Ploščina trikotnika, izražena s polmerom R trikotniku očrtanega kroga:
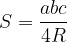
Če imamo podani dve stranici in kot med njima, ploščino trikotnika računamo po naslednjih enačbah:
Ploščina trikotnika, izražena s stranicama trikotnika in kotom med njima:
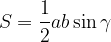
pri čemer sta 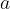 in
in 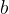 stranici trikotnika,
stranici trikotnika, 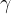 pa kot med njima;
pa kot med njima;
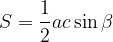
pri čemer sta 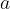 in
in  stranici trikotnika,
stranici trikotnika, 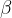 pa kot med njima;
pa kot med njima;
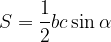
pri čemer sta 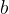 in
in  stranici trikotnika,
stranici trikotnika, 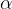 pa kot med njima.
pa kot med njima.
Ploščina za posebne primere trikotnika se glasi:
Ploščina enakostraničnega trikotnika:
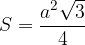
Ploščina pravokotnega trikotnika:
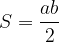
pri čemer sta a in b kateti pravokotnega trikotnika.
Z izreki, opisanimi v nadaljevanju, na podlagi poznanih kotov in/ali stranic ugotavljamo neznane kote in/ali stranice. Omenjeni postopek imenujemo razreševanje trikotnika.
Kosinusni izrek zapišemo z naslednjimi enačbami:
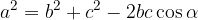
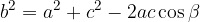
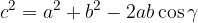
Z zgornjimi enačbami lahko ob podanih
dveh stranicah in
kotu med njima
izračunamo tretjo stranico.
Z ustreznim obračanjem zapisanih enačb pa lahko ob podanih vseh treh stranicah izračunamo kateri koli notranji kot v trikotniku.
Sinusni izrek se glasi:
V trikotniku velja, da je razmerje med sinusom katerega koli kota in dolžino njemu nasproti ležeče stranice konstantno in enako dvakratni vrednosti polmera trikotniku očrtanega kroga 2R:
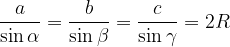
Vedno izberemo tako enakost, da si lahko z njo pomagamo: če imamo na primer podani stranici a in c ter kot 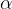 , iščemo pa kot
, iščemo pa kot 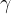 , bomo uporabili naslednjo enačbo:
, bomo uporabili naslednjo enačbo:
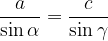
S sinusnim izrekom lahko ob podanih
dveh stranicah in
kotu nasproti ene izmed njih
izračunamo kot nasproti drugi stranici.
Ob podanih
dveh kotih in
stranici nasproti enemu izmed njih
lahko izračunamo stranico nasproti drugemu kotu.
Ob podanem radiju trikotniku očrtanega kroga pa lahko:
za kateri koli podani kot izračunamo dolžino nasprotno ležeče stranice oziroma
za katero koli podano stranico izračunamo velikost nasproti ležečega kota.