Prijava z e-naslovom
Prijava brez gesla
Za naravna števila smo povedali, da so to števila, s katerimi štejemo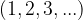 
.
Ko štejemo, število vedno povečujemo za 1. Če neko število povečujemo za vrednost števila samega, pa dobimo njegove večkratnike.
Večkratnike nekega števila lahko dobimo tudi z zaporednim množenjem tega števila naravnimi števili od 1 naprej.
Večkratniki določenega števila so zmnožki tega števila z naravnimi števili od 1 naprej.
Najmanjši večkratnik števila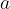 
je število 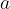, največjega večkratnika števila pa ne moremo določiti. Ker lahko izbrano število 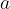množimo z neskončno mnogo naravnimi števili, je neskončno mnogo tudi njegovih večkratnikov.
Večkratnike števila a zapišemo kot množico, ki jo označimo z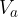 
.
Večkratnik števila 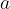je vsako število 
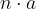, pri čemer je 
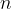poljubno naravno število. Množico večkratnikov označimo z :
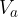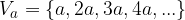
Vsako število ima različne večkratnike, na vsake toliko pa se zgodi, da se večkratniki različnih števil "ujamejo". Te večkratnike imenujemo skupni večkratniki.
Večkratniki nekega števila 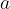so zmnožki tega števila z naravnimi števili. Zato pri deljenju večkratnika števila 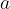s številom 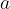samim ni ostanka.
Večkratnik poljubnega števila 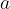je deljiv s številom .
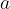Če se zgodi, da je neko število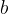 
deljivo z dvema ali več števili, potem je število 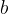skupni večkratnik teh števil.
Skupni večkratnik več števil je hkrati deljiv z vsakim od teh števil.
Vemo, da ima vsako število neskončno večkratnikov, zato največji skupni večkratnik dveh ali več števil ne obstaja. Lahko pa poiščemo najmanjši skupni večkratnik, zato bo ta za nas še posebej zanimiv.
Najmanjši skupni večkratnik števil 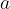in 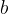zapišemo kot 
.
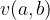Najmanjši skupni večkratnik poiščemo lahko tudi za več števil.
Pri večjih številih metoda s številsko premico postane nepregledna, zato se spomnimo na relacijo deljivosti, ki pravi, da je skupni večkratnik danih števil tisto število, ki je hkrati deljivo z vsakim od teh števil.
Trditev lahko zapišemo tudi za najmanjši skupni večkratnik:
Najmanjši skupni večkratnik dveh ali več števil je najmanjše število, ki je hkrati deljivo z vsakim od teh števil.
Kako pa bi našli najmanjši skupni večkratnik dveh večjih števil 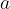in 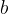? Če je najmanjši skupni večkratnik dveh večjih števil deljiv z njima, potem je deljiv tudi z vsemi njunimi delitelji. Deljiv je tudi z vsemi njunimi prafaktorji.
Zato se moramo najprej osredotočiti na vsako od števil 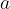in 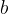in poiskati njune sestavne dele - prafaktorje. Potem pa bomo z njimi sestavili še njun najmanjši skupni večkratnik.
Če je neko število 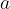deljivo s številom 
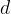, potem je deljivo tudi z vsemi prafaktorji, ki sestavljajo število .
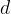Preverimo to trditev v naslednjem primeru:
Imejmo torej v mislih, da lahko vsako večje število razstavimo na produkt prafaktorjev.
Zato bomo tudi najmanjši skupni večkratnik števil iskali tako, da bomo vsako število najprej razstavili na prafaktorje. Najmanjši skupni večkratnik teh števil bomo nato sestavili kot produkt prafaktorjev.
Najmanjši skupni večkratnik števil je produkt vseh različnih prafaktorjev posameznih števil z najvišjo stopnjo potence.
