Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Štirikotnik je ortodiagonalen, če se njegovi diagonali sekata pod pravim kotom. Ploščina poljubnega ortodiagonalnega štirikotnika z dolžinama diagonal e in f je enaka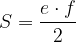 
.
Naj bodo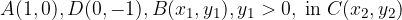 
take točke na enotski krožnici, da je štirikotnik ABCD trapez z osnovnicama AB in CD. Diagonali trapeza se sekata v točki P.
Označimo z O izhodišče koordinatnega sistema in s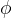 
velikost kota AOB.
Dokažite, da je trapez ABCD enakokrak. Narišite skico.
Izračunajte velikosti kotov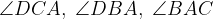 
in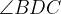 
ter dokažite, da je trapez ABCD ortodiagonalen.
Koordinati točke B ter dolžino diagonale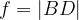 
izrazite s .
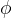Ploščino trapeza ABCD izrazite s 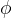. Katero točko B na enotski krožnici bi morali izbrati, da bi bila ploščina trapeza ABCD največja? Odgovor utemeljite.
in 
.
in 
enaka, iz česar sledi, da sta oba kota ob osnovnici CD enaka, torej je trapez enakokrak.
in 
obodna kota kotu 
nad lokom tetive AD. Torej sta kota enaka in merita 
.
in 
nad lokom tetive AB. Torej sta kota enaka in merita 
.
. Ta kot ustreza točki z y koordinato 1, zapišemo:
