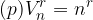Osebne zbirke


Variacije so razporeditve, podobne kot permutacije. Na razpolago imamo n različnih elementov, vendar pa v vrsto ne razporedimo vseh, pač pa le r od njih.
Variacije so torej razporeditve n elementov na r mest. Pri tem velja, da je n > r, torej število elementov je vedno večje od števila mest, na katera bomo razporedili te elemente.
Vrstni red pri variacijah je pomemben.
Variacijah brez ponavljanja uporabimo, ko želimo n različnih elementov razporediti na r prostih mest. Pri tem velja, da je r < n in po razporeditvi ugotovimo, da ostane nekaj elementov nerazporejenih.
Pri variacijah brez ponavljanja lahko na r prostih mest razporedimo le r od n različnih elementov.
Število vseh možnih variacij brez ponavljanja izračunamo na naslednji način:
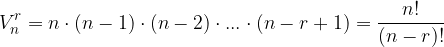
Variacije s ponavljanjem uporabimo, ko želimo n elementov, ki niso nujno različni, razporediti na r prostih mest. Pri tem velja, da se lahko en element pojavi na več mestih hkrati.
Pri variacijah s ponavljanjem lahko na r prostih mest razporedimo elemente n različnih vrst.
Število vseh možnih variacij s ponavljanjem izračunamo na naslednji način: