Osebne zbirke


V vsakodnevnih pogovorih pogostokrat izražamo svojo oceno, kolikšna je verjetnost, da se bo nek dogodek zgodil, npr: "Stoprocentno sem prepričan, da bom dobil povišico.", "Zagotovo bo danes deževalo.", "Nemogoče je, da ji ne bi uspelo!" itn. V teh stavkih izražamo svoja prepričanja o izzidu nekega slučajnega dogodka. Pri tem je slučajen dogodek dogodek, katerega obstoj ne moremo ali ne znamo zagotovo predvideti vnaprej: lahko se zgodi, lahko pa tudi ne.
Z izrazi o verjetnosti v osnovi ocenjujemo ali se bo nek slučajni dogodek zgodil ali ne. Glede na to, kako pogosto se dogodek zgodi, in koliko poskusov moramo pri tem izvesti, danemu dogodku priredimo "njegovo" verjetnost. Le-to verjetnost, namesto da jo ocenjujemo subjektivno, lahko matematično izračunamo mnogo bolj konkretno.
Verjetnost dogodka je število, ki označuje kolikšna je možnost, da se bo v enem poskusu zgodil nek dogodek oziroma ali se bo nek dogodek sploh zgodil ali ne.
Verjetnost označujemo z veliko črko P, posamezne dogodke pa vedno poimenujemo. Tako verjetnost dogodka, ki ga poimenujemo s črko A označimo z:
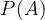
Verjetnost nemogočega dogodka N je vedno enaka 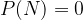 , verjetnost gotovega dogodka G pa je vedno enaka
, verjetnost gotovega dogodka G pa je vedno enaka 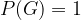 .
.
Za verjetnost poljubnega dogodka A velja:
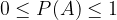
Obstaja več matematičnih metod določanja verjetnosti dogodka. Mi bomo spoznali dve, statistično definicijo verjetnosti in klasično definicijo verjetnosti.
V gradivu Verjetnostni račun smo govorili o dogodkih in poskusih; na hitro ponovimo: poskus je npr. met kovanca. Dogodek je rezultat poskusa, v primeru meta kovanca imamo dva možna dogodka: pade grb ali pade cifra. Dogodka sta enakovredna, saj obstaja enaka možnost, da pade grb ali da pade cifra.
Poskus lahko večkrat ponovimo in pri tem štejemo kolikokrat se je zgodil izbrani dogodek, ki naj bo poimenovan kot dogodek A (npr. pade grb). Razmerje med:
številom poskusov, v katerih se je zgodil dogodek A in
številom vseh ponovitev poskusa
imenujemo relativna frekvenca dogodka A. Relativna frekvenca dogodka je število, ki ga priredimo danemu poskusu.
Relativna frekvenca dogodka je razmerje med številom realizacij dogodka A (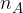 ) in številom vseh poskusov
) in številom vseh poskusov 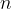 :
:
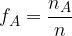
Poglejmo še enkrat zgoraj podani primer in zapišimo nekaj opazk:
čeprav mečemo pošten kovanec, kjer je v teoriji verjetnost (oziroma relativna frekvenca dogodka) za grb ali cifro enaka, torej 0.5, s končnim številom poskusov skoraj nikoli ne dobimo natančne vrednosti 0.5;
večje kot je število poskusov, bolj se dobljena relativna frekvenca dogodka (recimo dogodka A) približuje teoretični vrednosti, torej 0.5, verjetnosti dogodka.
Obe ugotovitvi pravzaprav nakazujeta zakon statistike, ki pravi, da se z naraščanjem števila ponovitev nekega poskusa, relativna frekvenca dogodka začne približevati nekemu številu, statistični verjetnosti dogodka A.
Statistična ali eksperimentalna verjetnost dogodka A je število, h kateremu se z naraščanjem ponovitev poskusa približuje relativna frekvenca dogodka A in se pri tem številu tudi ustali.
Lahko rečemo, da je statistična verjetnost dogodka A število, pri katerem se - ob dovolj velikem številu poizkusov - ustali razmerje med 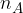 številom realizacij dogodka A in
številom realizacij dogodka A in 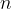 številom izvedenih poskusov.
številom izvedenih poskusov.
Računanje verjetnosti nekega dogodka na tak empiričen način (s poskusi) je okorno, navadno zahteva veliko časa, velikokrat tudi dlje, kot traja človeško življenje. Zato je pri iskanju načina, kako verjetnost nekega dogodka izračunati brez izvajanja poskusov, francoski matematik Laplace, določil teoretično formulo verjetnosti, ki jo dandanes imenujemo klasična definicija verjetnosti.
Klasična ali teoretična definicija verjetnosti pravi: če so vsi elementarni dogodki nekega vzorčnega prostora enako verjetni (enakovredni), in je dogodek A sestavljen dogodek iz elementarnih dogodkov iz tega vzorčnega prostora, je verjetnost dogodka A enaka:
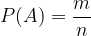
kjer je m število ugodnih elementarnih dogodkov za dogodek A in n število vseh elementarnih dogodkov poskusa.
Tako kot statistična definicija verjetnosti tudi klasična definicija verjetnosti velja le v vzorčnem prostoru poskusa, kjer so vsi njegovi elementarni dogodki med seboj enakovredni in s tem enako verjetni. Tak vzorčni prostor imenujemo simetričen vzorčni prostor.
Obe definiciji verjetnosti dogodkov v simetričnem vzorčnem prostoru, tako statistična kot tudi klasična definicija, imata skupne naslednje lastnosti, ki jih imenujemo aksiomi verjetnosti.
Aksiomi verjetnosti:
Verjetnost slučajnega dogodka A je nenegativno število:
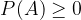
Verjetnost gotovega dogodka G je enako 1:
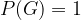
Verjetnost vsote nezdružljivih dogodkov A in B; če velja 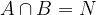 , je enaka vsoti verjetnosti posameznih dogodkov:
, je enaka vsoti verjetnosti posameznih dogodkov:
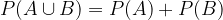
Kako računamo vsoto dveh združljivih dogodkov A in B; torej, ko njun presek ni ničelen, si bomo ogledali v naslednjem poglavju Računanje verjetnosti.
Verjetnost nemogočega dogodka N je enako 0:
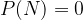
Verjetnost dogodku A nasprotnega dogodka A', je enaka 1 - verjetnost dogodka A:
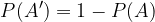
To poglavje je namenjeno zahtevnejšim bralcem. Poglavje lahko bralec izpusti brez škode za razumevanje celotnega poglavja.
Kot smo že omenili, klasična definicija verjetnosti velja le v simetričnem vzorčnem prostoru poskusa, kjer so vsi njegovi elementarni dogodki enako verjetni.
Z upoštevanjem aksiomov verjetnosti in lastnosti vzorčnega prostora izpeljemo verjetnost dogodka v simetričnem vzorčnem prostoru.
Naj bodo
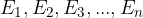
elementarni dogodki nekega poskusa. Očitno velja, da je njihova vsota gotov dogodek:
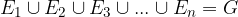
Ker velja, da so elementarni dogodki paroma nezdružljivi, jih lahko zapišemo z aksiomom verjetnosti (3):
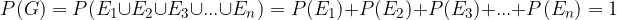
Ker so vsi elementarni dogodki simetričnega vzorčnega prostora enakovredni, velja:
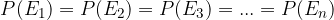
Iz česar sledi:
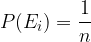
Če torej za dogodek A velja, da ima m ugodnih elementarnih dogodkov, potem je njegova verjetnost res enaka:
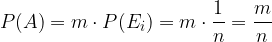
Znamo izračunati verjetnost dogodka v simetričnem vzorčnem prostoru. A včasih je simetričnost vzorčnega prostora nekega poskusa težko zagotoviti, iz česar sledi, da je klasična definicija verjetnosti dogodka zelo omejena. Za tipičen primer omejitve lahko vzamemo računanje verjetnosti dogodka pri metu goljufive kocke: ker se verjetnosti, da dobimo izbrano število pik, med seboj razlikujejo, očitno ne gre več za simetričen vzorčni prostor.
Zato za računanje verjetnosti dogodkov iz nesimetričnih vzorčnih prostorov - takih, kjer imajo elementarni dogodki lahko različne verjetnosti - upoštevamo aksiomatično definicijo verjetnosti ruskega matematika Kolgomorova, ki verjetnost dogodka definira kot funkcijo na vzorčnem prostoru.
Aksiomatična definicija verjetnosti definira verjetnost kot preslikavo, ki vsakemu elementarnemu dogodku iz množice vseh dogodkov nekega poskusa priredi realno število, če zadošča pravilom treh aksiomov Kolgomorova.
Aksiomi Kolgomorova so lastnosti, ki veljajo za vse definicije verjetnosti (klasično, statistično, aksiomatično ...), in pravijo:
Funkcija je pozitivna:
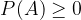
Funkcija je normirana:
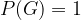
Če velja 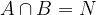 , potem velja:
, potem velja:
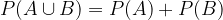
Ker te lastnosti veljajo za poljubne definicije verjetnosti, dani aksiomi veljajo tudi za računanje verjetnosti dogodkov, ko vzorčni prostor ni simetričen. V tem primeru velja, da so verjetnosti elementarnih dogodkov različne.
Izračun verjetnosti dogodka iz nesimetričnega vzorčnega prostora 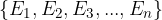 je mogoč le v primeru, da so znane posamezne verjetnosti elementarnih dogodkov
je mogoč le v primeru, da so znane posamezne verjetnosti elementarnih dogodkov 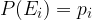 . Tako kot za verjetnosti dogodkov iz simetričnega vzorčnega prostora, mora tudi za verjetnosti teh elementarnih dogodkov veljati:
. Tako kot za verjetnosti dogodkov iz simetričnega vzorčnega prostora, mora tudi za verjetnosti teh elementarnih dogodkov veljati: