Osebne zbirke


Z viskoznostjo smo se že srečali v poglavju Bernoullijeva enačba. Tukaj jo bomo spoznali nekoliko podrobneje.
Viskoznost je lastnost tekočin, ki pozvroči:
da je ovirano gibanje same tekočine ali
zaviralno silo na telo, ki se giblje v (viskozni) tekočini.
O zavorni sili na telo, ki se giblje v tekočini tem smo se že podučili v gradivu Bernoullijeva enačba, kjer smo zakon poimenovali kvadratni zakon upora.
A vrnimo se k viskoznosti: kako se kaže v naravi? Poglejmo si nekaj primerov.
Primeri kažejo vpliv različnih viskoznosti na fizikalne lastnosti tekočin. Zaradi manjše viskoznosti teče voda hitreje od olja ali medu. Zaradi velike viskoznosti mešamo med le z veliko težavo. Viskoznost medu se zmanjša, če ga segrejemo. Podobno velja tudi za druge kapljevine. Segreto olje je manj viskozno od hladnega. Zaradi viskoznosti je tok reke hitrejši na sredini struge kot pri bregu in hitrejši na gladini kot na dnu.
Viskoznost se kaže kot notranje trenje med plastmi gibajoče tekočine. Pri tem je vseeno, ali se giblje tekočina glede na mirujočo strugo (ali cev) ali pa se giblje predmet v mirujoči tekočini. V primeru, da teče voda po cevi, je hitrost vode tik ob cevi enaka nič, največja pa je v središču cevi. Enako velja za gibajoči čoln na mirujoči vodi: plast vode se tik ob čolnu giblje z enako hitrostjo kot čoln, če se odmikamo od čolna, pade hitrost vode na nič.
Mehanizem notranjega trenja ni enak mehanizmu, kot smo ga spoznali v poglavju Sila trenja in lepenja. V tekočinah ni sile lepenja, ki jo moramo premagati, da se prične telo gibati. Zavorna sila, ki jo povzroča viskoznost, je sorazmerna hitrosti. Če je hitrost nič, je tudi zavorna sila enaka nič.
Definirajmo viskoznost:
Viskoznost je merilo odpora tekočine proti strižni napetosti, ki delujejo na plasti tekočine med gibanjem.
Stavek potrebuje nekaj več razlage, zato si oglejmo poskus, prikazan na sliki 2. Pripeljal nas bo do enačbe, s katero določamo viskoznost.
Vzemimo tekočino majhne globine h, na katero položimo ravno ploščo površine S tako, da se ravno dotika gladine (glej sliko 2). Ploščo vlečemo po gladini s silo F tako, da se giblje z majhno hitrostjo v.
Izkaže se, da se z enako hitrostjo v giblje tudi plast tekočine, ki je neposredno pod ploščo. Zgleda, kot da je prilepljena na ploščo - ali če povemo drugače: plošča hoče "odstriči" zgodnjo plast tekočine od ostale tekočine. Od tod tudi izraz strižna sila.
Strižne sile delujejo tudi med vsemi ostalimi plastmi. Narava teh sil je naslednja:
V primeru kapljevin so to privlačne medmolekularne sile. Te sile se s temperaturo manjšajo.
V primeru plina ni privlačnih medmolekulatnih sil. V tem primeru se gibanje molekul plina zaradi temperature preko trkov (difuzije) prenaša iz ene plasti na drugo. Ker so strižne sile med plastmi posledica termičnega gibanja, pričakujemo, da bodo sile večje pri večjih temperaturah in padle na nič pri temperaturah blizu absolutne ničle.
Naštete sile so dokaj slabotne, zato prenos gibanja na naslednjo plast ni popolen. Naslednja plast nikoli ne bo dosegla hitrosti prejšnje plasti. Gibanje se tako prenaša iz plasti na plast tako, da vsaki naslednji plasti hitrost nekoliko upade. Na dnu se zadnja plast "prilepi" na mirujočo podlago in zato tudi miruje (glej izrisane vekorje hitrosti na sliki 2).
Pri vodi, olju, zraku opazimo, da hitrost dejansko linearno pada od gibajoče plošče do mirujočega dna. Pogoj je, da sta globina h in hitrost v majhna. Tekočine, ki se obnašajo v skladu s to ugotovitvijo, se imenujejo newtonske tekočine (po fiziku Isaacu Newtonu). Ta zakonitost pa ni značilna za vse tekočine; odvisnost hitrosti od globine je lahko nelinearna.
Newton je podal enačbo odvisnosti količnika F/S od količnika v/h in velja za newtonske tekočine:
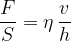
Pri tem velja:
Faktor 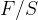 je strižna napetost. Enačba je enaka kot za tlak, le da namesto pravokotno (kot pri tlaku) deluje sila v smeri ploskve. Enota je enaka kot za tlak, torej:
je strižna napetost. Enačba je enaka kot za tlak, le da namesto pravokotno (kot pri tlaku) deluje sila v smeri ploskve. Enota je enaka kot za tlak, torej:
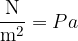
Faktor 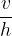 se imenuje strižna hitrost.
se imenuje strižna hitrost.
Faktor sorazmernosti 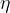 se imenuje viskoznost.
se imenuje viskoznost.
Viskoznost izrazimo iz zgornje enačbe:
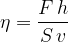
njena enota pa je:
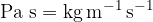
V naslednji tabeli so podane viskoznosti in gostote nekaterih snovi pri temperaturi 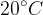 in tlaku 1 bar:
in tlaku 1 bar:
Viskoznost je sorazmernostni koeficient med strižno napetostjo 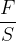 in strižno hitrostjo
in strižno hitrostjo 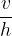 :
:
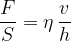
Enota za viskoznost je 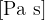 (Paskal sekunda).
(Paskal sekunda).
Majhen predmet je popolnoma potopljen v mirujoči, viskozni tekočini in se v njej počasi giblje (lahko se giblje tudi tekočina, predmet pa miruje). Zahteva, da je predmet majhen in hitrost majhna je podana zato, da ne bo gibajoči predmet povzročil vrtinčenja tekočine, kar bi povečalo upor.
Kot smo se naučili že v prejšnjem poglavju, se bo plast tekočine tik ob gibajočem predmetu gibala z enako hitrostjo kot predmet (glej vektorje hitrosti - rdeče puščice - na sliki 3). Plast tekočine tik ob telesu bo delovala s strižno silo na sosednjo plast tako, da se bo ta pričela gibati z nekoliko manjšo hitrostjo. Hitrost vsake sosednje plasti je nekoliko nižja - zato plasti tekočine, ki so dovolj stran od predmeta, mirujejo (gibanje predmeta nanje ne vpliva).
V gornjem poglavju smo ugotovili, da:
za ploščo s površino S,
ki se giblje po gladini s hitrostjo v,
v viskozni tekočini z globino h
velja Newtonova enačba:
Sila upora je premo sorazmerna hitrosti, zato je to linearni zakon upora.
V primeru, da velja linearni zakon upora, lahko zapišemo silo upora tekočine na telo s splošno enačbo:
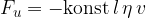
kjer je 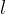 dolžina v čelnem preseku telesa.
dolžina v čelnem preseku telesa.
Zares je izpeljava sile linearnega upora za konkretno telo precej zahtevno. Na tem mestu brez izpeljave zapišimo, da za kroglico z radijem r velja:
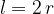
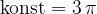
Sila upora na kroglico, ki se giblje v viskozni tekočini je torej:
Za majhno telo, ki se giblje z majhno hitrostjo v v viskozni tekočini z viskoznostjo 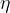 , velja linearni zakon upora:
, velja linearni zakon upora:
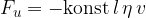
kjer je l dolžina v čelnem preseku telesa (pri krogli je ta dolžina 2r).
Za majhno kroglico se zakon linearnega upora glasi:
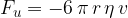
Večkat smo v dilemi, ali moramo pri računanju sile upora uporabiti linearni ali kvadratni zakon upora. Za uporabo enega ali drugega zakona se odločamo na osnovi izračuna Reynoldsovega števila Re. Izračunamo ga po enačbi:
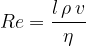
Pri tem je 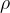 gostota tekočine. V primeru krogle vzamemo
gostota tekočine. V primeru krogle vzamemo 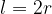 in dobimo:
in dobimo:
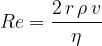
Z Reynoldsovim številom se ravnamo po naslednjih pravilih:
Če je Re < 0,5, uporabimo linearni zakon upora.
Če je Re > 1000, uporabimo kvadratni zakon upora.
Če je Re v vmesnem področju, ne velja noben od teh dveh zakonov
Reynoldsovo število za kroglo z radijem r, ki se giblje s hitrostjo v v tekočini z viskoznostjo 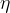 in gostoto
in gostoto 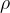 , izračunamo s pomočjo enačbe:
, izračunamo s pomočjo enačbe:
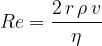
S pomočjo Reynoldsovega števila preverjamo ali velja linearni ali kvadratni zakon upora. Če je Re<0,5, uporabimo linearni zakon upora, če je Re>1000, uporabimo kvadratni zakon upora, pri vmesnih rezultatih ne velja noben od teh dveh zakonov.