Prijava z e-naslovom
Prijava brez gesla
Vzajemno delovanje sil je prisotno vsepovsod. Če potisnemo z roko ob steno hiše, čutimo, da tudi stena deluje nazaj na našo roko. Zemlja s silo teže privlači jabolko, ki visi na drevesu, a vendar tudi jabolko privlači Zemljo. Telesa delujejo druga na drugo - vzajemno.
Sile lahko medsebojno delujejo:
preko dotika. Npr. svinčnik leži na mizi. S svojo težo pritiska na mizo, a hkrati miza pritiska nazaj na svinčnik.
na daleč. Npr. sonce deluje na planete, ki so oddaljeni. Na planete deluje z enako silo kot planeti delujejo nazaj na Sonce.
To je zakon o vzajemnem delovanju sil, znan tudi kot 3. Newtonov zakon. Če 3. Newtonov zakon povzamemo na kratko, ta pravi: akcija je enaka reakciji.
S pomočjo zakona o vzajemnem delovanju sil si lahko razložimo tudi notranje sile. Poglejmo si primer.
Poglejmo si podrobneje pojave, ki smo jih pravkar opisali.
3. Newtonov zakon pravi, da sile delujejo vzajemno. Učinek vzajemnega delovanja sil bomo najlažje spoznali na primerih.
Na primerih spoznavamo zakonitosti o medsebojnem delovanju sil, poznano tudi kot 3. Newtonov zakon. Telesa vedno vzajemno delujejo druga na drugo. Lahko je to delovanje preko medsebojnega dotika ali pa tudi na daleč.
Slika 2: Zemlja deluje na Mesec z nasprotno in po velikosti enako silo, kot Mesec na Zemljo.
Zakon o medsebojnem delovanju sil ali 3. Newtonov zakon se glasi: telesa delujejo druga na drugo vzajemno. Če deluje prvo telo na drugega s silo F, bo drugo telo delovalo na prvega z nasprotno silo -F.
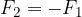
Vzemimo lahko vrvico, na katero je obešena utež. Vrvica je pripeta na strop. Utež deluje navzdol s silo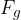 
. Na mestu, kjer je pripeta vrvica na strop deluje sila, nasprotna sili teže in usmerjena navzgor. Imenujmo jo silo stropa 
.
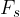Opazimo, da je vrvica je napeta iz česar sklepamo, da tudi v vrvici delujejo sili. To sta nasprotni sili teže in stropa; ker delujeta v sami vrvici, ji pravimo notranji sili. Ker vrvica miruje, sta notranji sili v ravnovesju (njuna rezultatna je enaka nič).
Slika 3: notranja sila vrvice.
Podobno velja za vse konstrukcije. Vzemimo npr. most. Če je most stabilen, je vsota sil v vsaki točki mostu enaka nič, tudi, če v opazovani točki deluje več sil.
Poznavanje notranjih sil v konstrukcijah je pomembno zato, saj s tem spoznamo, kakšne obremenitve lahko prenesejo. Na primer: most mora, poleg osnovne obremenitve (to je npr. teža same konstrukcije) prenesti še dodatne obremenitve (npr. tovornjak na mostu). Konstrukcija mora biti taka, da pri največji predvideni obremenitvi ne prekoračimo meje trdnosti materialov, iz katerih je zgrajena konstrukcija.
Vzemimo elastično vzmet in nanjo delujmo s silo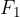 
, kot kaže slika 4, levo:
Slika 4: sila na vzmet.
Vzmet se razteza vse dokler ni vsota notranjih sil v vzmeti enaka nič. Takrat se raztezanje ustavi in je sila vzmeti enaka vlečni sili:
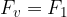
Ravnovesje se vzpostavi pri raztezku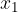 
. Z merjenji ugotovimo, da je velikost vlečne sile premosorazmerna z raztezkom vzmeti:
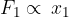
Kolikšen bo ta raztezek pri določeni sili zavisi tudi od trdote vzmeti: pri mehkejši vzmeti bo pri enaki sili raztezek večji. Sorazmernostni faktor med silo in raztezkom označimo s k in ga imenujmo koeficient vzmeti. Zapišemo enačbo brez indeksov:
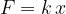
Napisana enačba se imenuje Hookov zakon. Iz Hookovega zakona izrazimo še koeficient k:
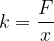
Enota za koeficient vzmeti je N/m.
Sila, s katero delujemo na elastično vrv ali vzmet je enaka sili, s katero se vzmet upira zunanji sili. Velja Hookov zakon:
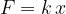
kjer je k koeficient vzmeti, ki predstavlja trdoto vzmeti.
Hookov zakon uporabljamo za merjenje sil s pomočjo vzmetne tehtnice. Vzmetna tehtnica vsebuje lahko vzmet na kateri je vrisano merilo, umerjeno kar v N.
Slika 5: vzmetna tehtnica.
Na sliki 5, levo lahko vidimo neobteženo vzmet. Vzmetna tehtnica na sliki ima merilno območje 0,1 do 1 N. Merne oznake, označene s črno črto, se nahajajo v razmaku po 0,1 N. Na tehtnico obesimo utež, slika 5, desno in odčitamo silo teže 0,5 N.
