Osebne zbirke


Zaporedje je funkcija: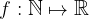 .
.
To pomeni, da poljubnemu naravnemu številu n pripada določeno realno število, ki ga označimo z 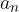 ,
, 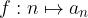 . Imenujemo ga n-ti člen zaporedja.
. Imenujemo ga n-ti člen zaporedja.
Če nas zanima element na nekem poljubnem mestu v zaporedju, v funkcijo f(n) vstavimo številko tega mesta in s tem dobimo vrednost elementa.
Zaporedje je posebna funkcija, zato namesto oznake 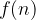 uporabljamo oznako
uporabljamo oznako 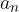 , vrednosti zaporedja pa označimo z
, vrednosti zaporedja pa označimo z 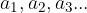 . Imenujemo jih členi zaporedja,
. Imenujemo jih členi zaporedja, 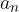 pa splošni člen.
pa splošni člen.
Zaporedje lahko predstavimo na 4 različne načine:
navedemo splošni člen zaporedja: 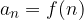
navedemo nekaj zaporednih členov zaporedja: 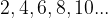
Rekurziven način: navedemo prvi člen ali prvih nekaj členov zaporedja, za ostale pa navedemo pravilo za računanje vsakega naslednjega člena, na podlagi prejšnjega člena oz prejšnjih členov: 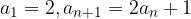
z množico vseh urejenih parov, ki sestavljajo graf zaporedja: 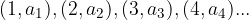 Graf geometrijsko ponazorimo v koordinatnem sistemu s točkami, katerih abcisa je n, ordinata pa
Graf geometrijsko ponazorimo v koordinatnem sistemu s točkami, katerih abcisa je n, ordinata pa 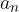 .
.
Zaporedju lahko določimo naslednje lastnosti: končnost/neskončnost, omejenost/neomejenost in naraščanje/padanje.
Zaporedje je končno, če je sestavljeno iz končno mnogo členov. Pri končnem zaporedju poznamo končni člen zaporedja in število vseh členov.
Zaporedje je neskončno, če je sestavljeno iz neskončno mnogo členov. Pri neskončnem zaporedju ne poznamo končnega člena zaporedja niti števila vseh členov.
Zaporedje je lahko navzgor omejeno, navzdol omejeno, omejeno na obe strani ali pa neomejeno.
Zaporedje je navzgor omejeno, če obstaja tako število 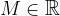 , da za vsak
, da za vsak 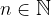 velja:
velja:
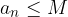
Število M imenujemo zgornja meja zaporedja.
Se pravi, če je zaporedje navzgor omejeno, pomeni, da so vsi členi zaporedja manjši ali enaki od nekega števila M.
Zaporedje je navzdol omejeno, če obstaja tako število  , da za vsak
, da za vsak 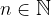 velja:
velja:
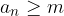
Število M imenujemo spodnja meja zaporedja.
Se pravi, če je zaporedje navzdol omejeno, pomeni, da so vsi členi zaporedja večji ali enaki od nekega števila m.
Zaporedje je omejeno, če obstajata taki števili 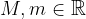 , da za vsak
, da za vsak 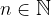 velja:
velja:
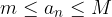
Se pravi, če je zaporedje omejeno, pomeni, da je navzgor in navzdol omejeno.
Zaporedje je neomejeno, če je navzgor in navzdol neomejeno.
Zaporedje je lahko naraščajoče, padajoče ali pa konstantno.
Zaporedje je naraščajoče, če za vsak 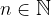 velja:
velja:
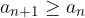
ali
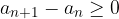
Se pravi, zaporedje je naraščajoče, če je vsak naslednji člen zaporedja večji ali enak predhodnemu. Če enačaj izpustimo, potem velja, da tako zaporedje strogo narašča.
Zaporedje je padajoče, če za vsak 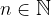 velja:
velja:
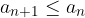
ali

Se pravi, zaporedje je padajoče, če je vsak naslednji člen zaporedja manjši ali enak predhodnemu. Če enačaj izpustimo, potem velja, da tako zaporedje strogo pada.
Zaporedje je monotono, če je ali naraščajoče ali padajoče.
Zaporedje je konstantno, če za vsak 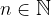 velja:
velja:
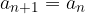
Se pravi, zaporedje je konstantno, če so vsi členi zaporedja med seboj enaki.
Zaporedje je alternirajoče, če si izmenoma sledijo pozitivni in negativni členi zaporedja.