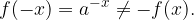Osebne zbirke


V tem poglavju bomo spoznali eksponentno funkcijo. To je funkcija, ki narašča bolj kot vsaka druga funkcija. Če opazujemo graf eksponentne funkcije na dovolj velikem območju, bo njena vrednost vedno presegla vrednost vsake druge funkcije.
Z njo lahko v naravi predstavimo razmnoževanje bakterij ali razpad atomov radioaktivnega elementa.
Definicija: eksponentna funkcija je vsaka funkcija, v kateri spremenljivka 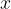 nastopa v eksponentu, osnova
nastopa v eksponentu, osnova 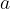 pa je pozitivna in različna od 1:
pa je pozitivna in različna od 1:
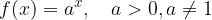
Eksponentne funkcije ne smemo mešati s potenčno funkcijo, v kateri je spremenljivka v osnovi potencirana z določenim številom. Primer potenčne funkcije:
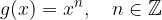
Eksponentne funkcije ločimo v dve večji družini.
Osnova je večja od 1:
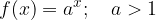
Osnova je med 0 in 1:
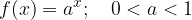
Osnova za ločitev obeh družin tiči v množenju: če množimo med seboj dve števili, ki sta večji kot 1, bo zmnožek večji od obeh števil. Če pa množimo med seboj dve števili, ki sta med 1 in 0, bo zmnožek manjši od obeh števil.
Poglejmo, kako sta obe vrsti povezani med seboj. Naj bo a > 1 in zapišimo funkciji:
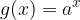
in

Funkcijo 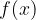 preoblikujmo tako, da bo osnova večja od 1:
preoblikujmo tako, da bo osnova večja od 1:
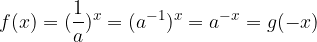
Naj bosta dani dve funkciji:
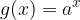

in velja naj, da je a > 1. Velja, da je:
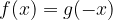
iz česar sledi, da sta grafa funkcij simetrična glede na ordinatno os (glej graf v naslednjem primeru).
To v kateri obliki je eksponentna funkcija podana vpliva na lastnosti funkcije in na izgled njenega grafa. Obravnavali bomo dve obliki eksponentne funkcije, osnovno in splošno.
Zaradi lastnosti funkcij, ki so skupne nekaterim eksponentnim funkcijam, imenujmo eksponentno funkcijo
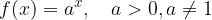
osnovna eksponentna funkcija, saj funkcija ni pomnožena s konstanto, ne vsebuje prostega člena in ni konstantna.
Najprej na konkretnem primeru narišimo graf osnovne eksponentne funkcije z osnovo večjo od 1, nato pa še z osnovo med 0 in 1.
Sedaj lahko čisto na kratko primerjamo grafa funkcij obeh družin, saj bomo lastnosti podrobneje predstavili v poglavju lastnosti. Obe funkciji imata:
enako definicijsko območje, zalogo vrednosti, spodnjo mejo
nista sodi in ne lihi
potekata skozi točko (0, 1)
sta bijektivni.
Prva od njiju je naraščajoča, druga padajoča.
Splošna obliko eksponentne funkcije je naslednja:
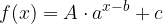
kjer je A pomeni razteg ali skrčitev grafa v smeri osi y, b premik v smeri osi x, c pa je prosti člen, ki pomeni premik grafa v smeri osi y.
Če je b < 0 graf premaknemo za b enot v levo, če je pa b > 0 graf premaknemo za b enot v desno.
Če je c < 0 graf premaknemo za c enot navzdol, če je pa c > 0 graf premaknemo za c enot navzgor.
Izkaže se, da vse lastnosti omenjene funkcije niso več enake kot pri osnovni eksponentni funkciji, zato si sedaj poglejmo njen graf, ki ga bomo primerjali z zgornjima grafoma.
Vidimo, da ima zgornji graf v primerjavi z grafoma osnovne eksponentne funkcije drugačno zalogo vrednosti, spodnjo mejo in ne poteka skozi točko (0, 1).
V družino eksponentnih funkcij, kjer je osnova > 0, spada tudi posebna eksponentna funkcija:
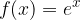
kjer je
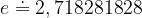
naravno število (ki spada v družino iracionalnih števil). Funkcijo 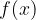 imenujemo naravna eksponentna funkcija.
imenujemo naravna eksponentna funkcija.
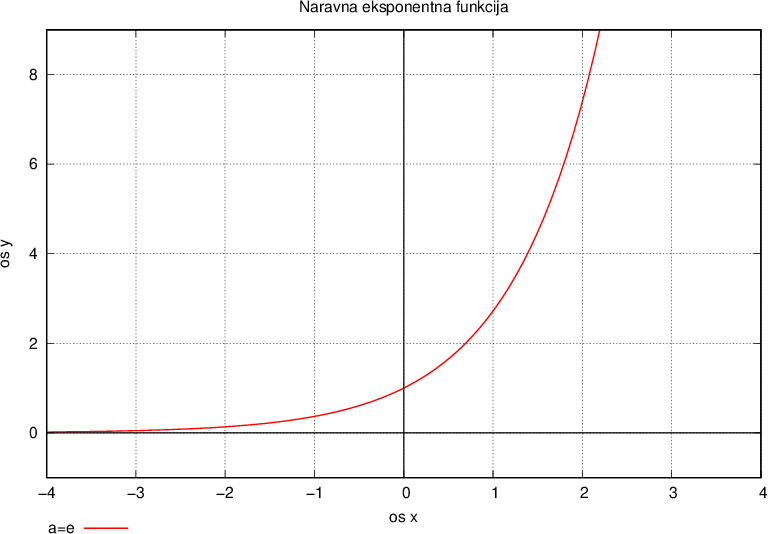
Naravna eksponentna funkcija je pomembna predvsem, v fiziki, saj se zelo pogosto pojavlja, ko opisujemo naravne pojave, npr: hitrost razpada radioaktivnih elemenetov.
Graf naravne eksponentne funkcije:
Ker se lastnosti eksponentne funkcije ločijo glede na to, ali je osnova večjo od 1 ali pa se nahaja med 0 in 1, bomo oba primera obravnavali posebej. Večji poudarek bomo namenili osnovnim eksponentnim funkcijam, saj imajo skupne lastnosti, ne glede na vrednost osnove a.
Lastnosti eksponentne funkcije je lažje razumeti, če si jo predstavljamo, zato si pomagajmo z grafi. Narišimo grafe funkcij z različnim osnovami.
Eksponentne funkcije z osnovo večjo od 1 so definirane za celotno množico naravnih števil:
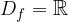
Zaloga vrednosti je množica pozitivnih realnih števil:
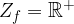
Iz grafa lahko enostavno razberemo, da je eksponentna funkcija, z osnovo a > 1, na celotnem definicijskem območju naraščajoča. Vemo, da je funkcija strogo naraščajoča, ko velja:

Eksponentna funkcija z osnovo a > 1, je na celotnem definicijskem območju strogo naraščajoča, saj za poljubni dve vrednosti:
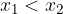
velja
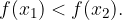
Velja tudi, da večja kot je osnova a, hitreje graf narašča.
Graf splošne eksponentne funkcije se približuje splošnemu členu c, ko vrednosti spremenljivke x padajo proti minus neskončnosti, zato je splošna eksponentna funkcija navzdol omejena s splošnim členom c:
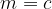
Ko vrednosti spremenljivke x naraščajo proti neskončnosti tudi graf spošne eksponentne funkcije narašča proti neskončnosti, zato funkcija navzgor ni omejena.
Spošna eksponentna funkcija je navzdol omejena s prostim členom c, navzgor pa ni omejena.
V primeru osnovne oblike, je prosti člen enak 0. Takrat je funkcija navzdol omejena z abscisno osjo.
Če v splošni obliki eksponentne funkcije nastopa tudi pozitivna konstanta A se meji ne spremenita, če pa negativna, pa se spremenita obe meji.
Funkcija je injektivna, ker se vsak x preslika v natanko en y.
Funkcija je surjektivna, ker vsakemu y pripada vsaj en x, ki se vanj preslika.
Funkcija je bijektivna, saj je injektivna in surjektivna.
Pri določanju Injektivnosti, surjektivnosti in bijektivnosti si lahko pomagamo tudi z vzporednicami abscisni osi. Več o tem, si lahko prebere v poglavju množice.
Vsem grafom osnovne eksponentne funkcije je skupno presečišče z ordinatno osjo, to je točka (0, 1).
V primeru splošne oblike pa naš graf funkcije več ne poteka skozi točko (0, 1).
Eksponentna funkcija 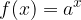 ni soda ker:
ni soda ker:
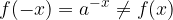
Eksponentna funkcija 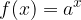 ni liha ker:
ni liha ker:
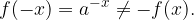
Podobno kot v prejšnjem poglavju bomo tudi tukaj narisali nekaj primerov eksponentne funkcije, da bomo potem lažje zapisali lastnosti te družine eksponentnih funkcij. Podrobneje se bomo posvetili splošnim eksponentnim funkcijam, saj imajo skupne lastnosti, ne glede na vrednosti osnove a.
Eksponentne funkcije z osnovo med 0 in 1 so definirane za vsa realna števila:
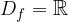
Zaloga vrednosti je množica pozitivnih realnih števil:
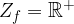
Iz grafa lahko enostavno razberemo, da je eksponentna funkcija na celotnem definicijskem območju padajoča. Vemo, da je funkcija strogo padajoča, ko velja:

Eksponentna funkcija z osnovo 0 < a < 1, je na celotnem definicijskem območju strogo padajoča, saj za poljubni dve vrednosti:
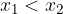
velja:
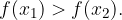
Velja tudi, da večja kot je osnova, počasneje graf pada.
Graf splošne eksponentne funkcije se približuje splošnemu členu c, ko vrednosti spremenljivke x naraščajo proti neskončnosti, zato je splošna eksponentna funkcija navzdol omejena s splošnim členom c:
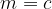
Ko vrednosti spremenljivke x padajo proti minus neskončnosti, graf splošne eksponentne funkcije narašča proti neskončnosti, zato funkcija navzgor ni omejena.
Spošna eksponentna funkcija je navzdol omejena s prostim členom c, navzgor pa ni omejena.
V primeru osnovne oblike, je prosti člen enak 0. Takrat je funkcija navzdol omejena z abscisno osjo.
Če v splošni obliki eksponentne funkcije nastopa tudi pozitivna konstanta A se meji ne spremenita, če pa negativna, pa se spremenita obe meji.
Funkcija je injektivna, ker se dva različna x-a preslikata v različna y-a.
Funkcija je surjektivna, ker vsakemu y pripada vsaj en x, ki se vanj preslika.
Funkcija je bijektivna, saj je injektivna in surjektivna.
Pri določanju Injektivnosti, surjektivnosti in bijektivnosti si lahko pomagamo tudi z vzporednicami abscisni osi. Več o tem, si lahko prebere v poglavju množice.
Vsem grafom osnovne eksponentne funkcije je skupno presečišče z ordinantno osjo, to je točka (0, 1).
V primeru splošne eksponentne funkcije, pa naš graf funkcije več ne poteka skozi točko (0, 1).
Eksponentna funkcija 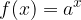 ni soda ker:
ni soda ker:
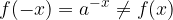
Eksponentna funkcija 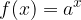 ni liha ker:
ni liha ker: