Prijava z e-naslovom
Prijava brez gesla
Spoznali smo že potence s celimi eksponenti. V tem gradivu nas bo pa zanimalo, kako lahko narišemo graf, v katerem "nastopa potenca". Takemu grafu pravimo potenčna funkcija, zapišemo pa jo z:
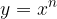
oziroma, zapisano bolj splošno:
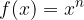
Pri tem je n celo število.
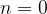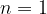Primerov, ko je n = 0 ali n = 1 ne bomo obravnavali, saj sta to posebna primera potenčnih funkcij, ki ju obravnavamo v ločenih gradivih (Linearna funkcija )
Potenčne funkcije bomo razdelili na dve družini:
Potenčne funkcije z pozitivnim (naravnim) eksponentom: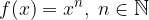 
Potenčne funkcije z negativnim celim eksponentom: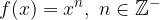 
Vsako izmed družin bomo obravnavali posebej.
Tudi to družino funkcij bomo razdelili na dve poddružini:
potenčne funkcije z naravnim sodim eksponentom
potenčne funkcije z naravnim lihim eksponentom
Vsako poddružino bomo obravnavali posebej, saj imajo potenčne funkcije v isti družini med seboj podobne lastnosti.
Sodo število n v splošnem zapišemo:
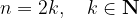
Torej: za katerikoli k, ki je naravno število, bo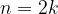 
sodo. Posledično potenčno funkcijo, ki ima naravni sodi eksponent, v splošnem zapišemo:
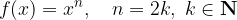
Skupne lastnosti potenčnih funkcij s pozitivnim sodim eksponentom bomo najlažje razumeli, če si najprej pogledamo nekaj konkretnih potenčnih funkcij.
Ob opazovanju slike iz gornjega primera, ugotovimo, da je graf potenčnih funkcij z naravnim sodim eksponentom parabola ; hkrati pa, da imajo te funkcije še nekatere druge enake lastnosti.
Lastnosti potenčnih funkcij oblike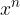 
, kjer je n pozitivni in sodi eksponent, so:
funkcija je definirana (obstaja) za vsak x, kar pomeni da predstavljajo definicijsko območje vsa realna števila. Matematično definicijsko območje (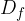
) potenčne funkcije zapišemo:
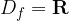
Zaloga vrednosti so vsi y, ki jih funkcija zajame; iz grafa lahko vidimo, da predstavljajo nenegativna realna števila. Matematično zalogo vrednosti (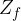
) potenčne funkcije zapišemo:
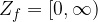
grafi potekajo vedno skozi tri skupne točke A(1,1), B(-1,1) in O(0,0);
imajo eno ničlo pri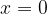 
;
so padajoče za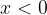 
in naraščajoče za 
;
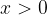najmanjša vrednost, ki jo funkcija doseže, je 0, kar pomeni da so funkcije navzdol omejene -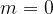 
pa predstavlja najmanjšo spodnjo mejo;
funkcija je soda, kadar je graf funkcije zrcalen glede na ordinatno os. Iz te definicije sklepamo, da so potenčne funkcije z naravnim sodim eksponentom sode funkcije;
niso bijektivne.
Liho število n v splošnem zapišemo:
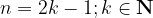
Torej: za katerikoli k, ki je naravno število, bo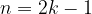 
liho. Posledično potenčno funkcijo, ki ima naravni lihi eksponent, v splošnem zapišemo:
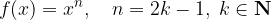
Tudi v tem primeru bomo skupne lastnosti potenčnih funkcij s pozitivnim lihim eksponentom najlažje razumeli, če si najprej pogledamo nekaj konkretnih potenčnih funkcij.
Ugotovimo, da imajo potenčne funkcije te družine med seboj podobne grafe (oblike sedla) in hkrati enake še nekatere druge lastnosti:
Lastnosti potenčnih funkcij oblike 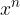, kjer je n pozitivni in lihi eksponent, so:
funkcija (f(x) ali y) je definirana (obstaja) za vsak x, kar pomeni da predstavljajo definicijsko območje vsa realna števila. Matematično definicijsko območje (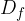) potenčne funkcije zapišemo:
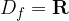
Zaloga vrednosti so vsi y, ki jih funkcija zajame; iz grafa lahko vidimo, da predstavljajo vsa realna števila. Matematično zalogo vrednosti (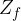) potenčne funkcije zapišemo:
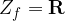
grafi potekajo vedno skozi tri skupne točke A(1, 1), B(–1, –1) in O(0, 0);
imajo eno ničlo pri ;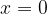
so povsod naraščajoče;
funkcije ne dosežejo najmanjše in tudi ne največje vrednosti, saj gredo v neskončnost. Temu pravimo, da je funkcija neomejena.
Funkcija je liha, kadar je graf funkcije zrcalen glede na koordinatno izhodišče. Iz te definicije sklepamo, da so potenčne funkcije z naravnim lihim eksponentom lihe funkcije.
so bijektivne funkcije.
Tudi to družino funkcij bomo razdelili na dve poddružini:
potenčne funkcije z negativnim sodim eksponentom
potenčne funkcije z negativnim lihim eksponentom
Vsako poddružino bomo obravnavali posebej, saj imajo potenčne funkcije v isti družini med seboj podobne lastnosti.
Tako kot prej, da bomo imeli jasno predstavo o družini funkcij, ki jo obravnavamo, se najprej spoznajmo z nekaj konkretnimi funkcijami iz te družine.
Če si ogledamo graf iz zadnjega primera, prepoznamo dve pomembni lastnosti:
Asimptota
Grafi funkcij se daleč od izhodišča približujejo abscisni osi in je nikoli ne dosežejo. Pravimo, da je abscisna os vodoravna asimptota teh funkcij.
Pol
Grafi funkcij v okolici koordinatnega izhodišča se zelo strmo dvigajo in približujejo k ordinatni osi - ki pa je nikoli ne dosežejo. Pravimo, da imajo funkcije pri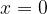 
pol. V polu funkcija ni definirana, poglejmo zakaj:
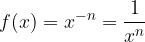
Opazimo, da če za x vstavimo 0, dobimo ulomek z imenovalcem 0. Vemo, da deljenje z 0 da nedefinirano vrednost. Očtino, skozi pol poteka navpična asimptota.
Asimptota je premica (lahko je vodoravna, poševna ali navpična), za katero velja, da se ji grafi funkcij v neskončnosti približujejo vendar je nikoli ne dosežejo. Ponavadi jo v koordinatnem sistemu označimo z črtkano premico.
Poli funkcije so območja, kjer funkcija ni definirana. Skozi vsak pol poteka navpična asimptota.
Ob opazovanju grafov opazimo še nekatere druge pomembne skupne lastnosti:
Lastnosti potenčnih funkcij z negativnim sodim eksponentom:
funkcija je definirana za vsak x razen za 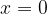, kar pomeni da predstavljajo definicijsko območje vsa realna števila brez števila 0. Matematično definicijsko območje zapišemo:
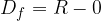
Zaloga vrednosti so vsi y, ki se pojavijo v grafu. Očitno so to samo pozitivna realna števila. Matematično zalogo vrednosti zapišemo:
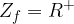
grafi potekajo skozi dve skupni točki 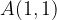A(1, 1) in B(–1, 1);
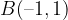imajo pol pri ;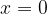
os x je vodoravna asimptota;
najmanjša vrednost, ki jo funkcija doseže je 0, iz česar sledi, da so navzdol omejene: ;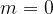
nimajo ničel;
so padajoče za 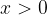in naraščajoče za ;
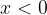grafi so zrcalni glede na ordinatno os - torej so funkcije sode;
niso bijektivne funkcije.
In spet, za boljšo predstavo, se najprej spoznajmo z nekaj konkretnimi funkcijami iz družine, ki jo obravnavamo.
Če si ogledamo graf iz zadnjega primera, prepoznamo dve pomembni lastnosti:
Asimptota
Grafi funkcij se daleč od izhodišča približujejo abscisni osi in je nikoli ne dosežejo. Pravimo, da je abscisna os vodoravna asimptota teh funkcij.
Pol
Grafi funkcij v okolici koordinatnega izhodišča se zelo strmo dvigajo / spuščajo in približujejo k ordinatni osi - ki pa je nikoli ne dosežejo. Pravimo, da imajo funkcije pri pol. V polu funkcija ni definirana, poglejmo zakaj:
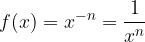
Opazimo, da če za x vstavimo 0, dobimo ulomek z imenovalcem 0. Vemo, da deljenje z 0 da nedefinirano vrednost. Očtino, skozi pol poteka hkrati navpična asimptota.
Ob opazovanju grafov opazimo še nekatere druge pomembne skupne lastnosti:
Lastnosti potenčnih funkcij z negativnim lihim eksponentom:
funkcija je definirana za vsak x razen za 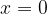, kar pomeni, da predstavljajo definicijsko območje vsa realna števila brez števila 0. Matematično definicijsko območje zapišemo:
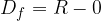
Zaloga vrednosti so vsi y, ki se pojavijo v grafu. Očitno so to vsa realna števila razen števila 0 (asimptoti se graf približuje, a je ne doseže). Matematično zalogo vrednosti zapišemo:
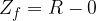
grafi potekajo skozi dve skupni točki A(1, 1) in B(–1, –1);
imajo pol pri ;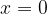
os x je vodoravna asimptota;
so povsod padajoče;
so neomejene;
grafi so zrcalni glede na koordinatno izhodišče - torej so funkcije lihe;
so bijektivne funkcije.
Z osnovnim grafom potenčne funkcije oblike:
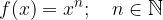
smo se že seznanili. V tem gradivu pa si bomo pogledali še grafe modificiranih potenčnih funkcij. Potenčne funkcije so lahko:
togo premaknjene v smeri ordinatne osi (premik grafa funkcije navzgor ali navzdol);
togo premaknjene v smeri abscisne osi (premik grafa funkcije v levo ali desno);
zrcaljene prek abscisne osi;
raztegnjene / skrčene vzdolž ordinatne osi.
V nadaljevanju si bomo te modifikacije podrobneje ogledali.
Naj bo dana že znana potenčna funkcija f(x). Kaj se zgodi, če znani funkciji prištejemo (ali odštejemo) neko realno število n?
Graf funkcije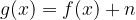 
dobimo tako, da (znani) graf funkcije f(x) togo premaknemo za n v smeri osi y:
navzgor, če je n > 0,
navzdol, če je n < 0.
Naj bo dana že znana potenčna funkcija f(x). Kaj se zgodi, če neodvisno spremenljivko x povečamo (ali zmanjšamo) za neko realno število k?
Graf funkcije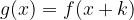 
dobimo tako, da (znani) graf funkcije f(x) togo premaknemo za k v smeri osi x:
v levo, če je k > 0,
v desno, če je k < 0.
Naj bo dana že znana potenčna funkcija f(x). Kaj se zgodi, če znani funkciji spremenimo predznak?
Graf funkcije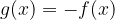 
dobimo tako, da (znani) graf funkcije f(x) prezrcalimo skozi x os.
Naj bo dana že znana potenčna funkcija f(x). Graf funkcije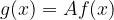 
dobimo tako, da graf funkcije f:
raztegnemo, če je A > 0
skrčimo, če je A < 0
za faktor A vzdolž osi y.
