Osebne zbirke


Kroženje je primer krivega gibanja. Pri kroženju se telo giba po obodu kroga, to je po krožni tirnici. Trenutno smer in hitrost njegovega gibanja opišemo z vektorjem hitrosti 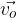 . Dali smo mu indeks o, saj gre za hitrost kroženja po obodu kroga. Pravimo mu tudi obodna hitrost kroženja.
. Dali smo mu indeks o, saj gre za hitrost kroženja po obodu kroga. Pravimo mu tudi obodna hitrost kroženja.
Vektor hitrosti sledi krožnici, zato se mu smer neprestano menja. Narišemo ga kot usmerjeno daljico, njegova smer pa je tangenta na krožnico v točki, kjer se telo trenutno nahaja (glej sliko 1).
Kroženje je glede na absolutno vrednost (velikost) hitrosti lahko:
enakomerno: absolutna vrednost vektorja hitrosti 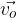 je konstanjtna - se ne spreminja s časom.
je konstanjtna - se ne spreminja s časom.
pospešeno: absolutna vrednost vektorja hitrosti 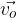 se v tem primeru spreminja s časom: lahko enakomerno narašča ali pa se enakomerno zmanjšuje. V tem primeru je to enakomerno pospešeno kroženje.
se v tem primeru spreminja s časom: lahko enakomerno narašča ali pa se enakomerno zmanjšuje. V tem primeru je to enakomerno pospešeno kroženje.
V tem poglavju bomo spoznali enakomerno kroženje.
Telo se giba enakomerno po krožni tirnici z radijem r, kot kaže slika 2.
S slike 2 lahko razberemo osnovne geometrijske elemente, s katerimi opisujemo kroženje:
vektor hitrosti 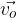 ali obodna hitrost je hitrost, s katero telo kroži po krožnici;
ali obodna hitrost je hitrost, s katero telo kroži po krožnici;
radij r krožnice, ki določa tir kroženja;
pot s, ki jo telo opravi v času t je enaka dolžini krožnega loka, ki ga med gibanjem opiše točka na krožnici;
kot 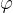 , ki ga telo opiše v času t.
, ki ga telo opiše v času t.
Poleg osnovnih geometrijskih elementov, pa pri kroženju nastopajo naslednje pomembne fizikalne veličine:
Obhodni čas
Telo se giblje po krožnici in po določenem času pride ponovno do izhodiščne točke, kjer se je začelo gibati. Času, ko telo naredi en obhod kroga, pravimo obhodni čas in ga označimo s 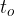 .
.
Obhodni čas je torej čas, v katerem točka ali telo naredi celoten obhod po krožnici in pride znova na začetno mesto.
Frekvenca kroženja
V splošnem nam frekvenca pove, koliko obhodov kroga naredi telo v opazovanem času. Ker pa običa pretvorimo enote v osnovne merske enote, nam frekvenca pove število obhodov, ki jih krožeča točka (npr. točka na ventilatorju) naredi v eni skundi. Oznaka za frekvenco je 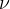 (izgovorimo ni).
(izgovorimo ni).
Kotna hitrost
Omenili smo že, da se med gibanjem telesa po krožnici spreminja tudi kot. Kako hitro kot narašča ali pada s časom, nam pove kotna hitrost. Pojem kotne hitrosti je podoben pojmu hitrosti, le da sedaj ne opazujemo opravljene poti v danem času, pač pa opisani kot v danem času. Pri kroženju uporabljamo za kot namesto stopinj raje enoto radian. Kotna hitrost nam torej pove, koliko radianov naredi kot v eni sekundi. Označimo jo z 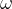 (izgovorimo omega).
(izgovorimo omega).
Radialni pospešek
Iz skice 2 opazimo, da se vektor hitrosti spreminja s časom (velikost morda ostaja ista, a se smer spreminja). Vemo, da je sprememba hitrosti v času enako pospešek.
Hitrost se spreminja zaradi radialnega pospeška. Radialni pospešek je tisti, ki omogoča, da se točka giba po krivem tiru - krožnici. Je usmerjen pravokotno na vektor obodne hitrosti in kaže v smeri radija.
Če bi krožeče telo nenadoma izgubilo radialni pospešek, bi nadaljevalo gibanje v smeri tangente na krožnico.
Obhodni čas, frekvenca in kotna hitrost so veličine, ki opisujejo podobne zakonitosti in izhajajo ena iz druge. Če poznamo izmed količin, poznamo tudi druge dve. Smiselno je, da jih spoznamo skupaj.
Obhodni čas je čas, v katerem točka naredi celoten obhod po krožnici in se znova pojavi na začetnem mestu. Označimo ga s 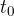 .
.
V obhodnem času tako posledično telo:
naredi pot, enako obsegu krožnice po kateri kroži: 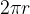 ;
;
in opiše polni kot 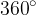 ali
ali 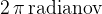 .
.
Frekvenca kroženja 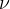 (izgovorimo ni) je izjemno tesno povezana z obhodnim časom:
(izgovorimo ni) je izjemno tesno povezana z obhodnim časom:
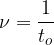
Enota za frekvenco je 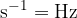 (Herz, izgovorimo herc).
(Herz, izgovorimo herc).
Frekvenco lahko izračunamo tudi tako, da preštejemo število obhodov krožnice N in jih delimo z opazovanim časom:
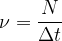
Opazujmo kot 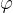 , ki ga opiše zveznica med opazovano točko in središčem kroga.
, ki ga opiše zveznica med opazovano točko in središčem kroga.
Kot se s časom, ko točka potuje po krožnici spreminja: narašča ali pada. Za koliko se kot poveča ali zmanjša v opazovanem času določa kotna hitrost 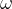 . Velja:
. Velja:
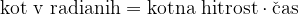
Zapišimo to z enačbo:
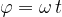
Kotno hitrost bolj splošno zapišemo:
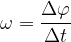
Enata za kotno hitrost je:
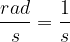
Radian smo spustili zato, ker ni fizikalna enota.
V enačbe kroženja vedno vstavljamo kot v radianih!
Ponovimo: kot lahko merimo v stopinjah ali pa v radianih. Če kot merimo v stopinjah, znaša celoten krog 360 stopinj. Če krog merimo v radianih, pa znaša poln krog 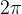 radianov. Razlika med stopinjami in radiani je le ta, da gre za različni merski enoti. Stopinje v radiane ali obratno pretvarjamo linearno, z enačbama:
radianov. Razlika med stopinjami in radiani je le ta, da gre za različni merski enoti. Stopinje v radiane ali obratno pretvarjamo linearno, z enačbama:
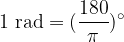
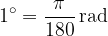
Več o stopinjah in radianih pa v gradivu merjenje v geometriji.
Izrazimo kotno hitrost s frekvenco. V ta namen uporabimo enačbo za kotno hitrost:
Pri enakomernem kroženju je kotna hitrost konstantna.
Ponovimo pojme in enačbe za točko, ki se enakomerno giblje po krožnici.
Obhodni čas 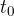 je čas enega obhoda krožnice.
je čas enega obhoda krožnice.
Kot je kotna hitrost krat čas:
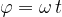
Frekvenca in obhodni časa sta recipročni:
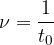
Frekvenca je tudi število obhodov N v opazovanem času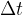 :
:
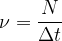
Kotno hitrost, obhodni čas in frekvenco povezujeta enačbi:
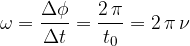
Pri enakomernem kroženju je kotna hitrost konstantna.
Obodna hitrost kroženja je hitrost, s katero se giba točka po krožnici. Pri enakomernem kroženju je gibanje po krožnici enakomerno, hitrost je konstantna, le smer hitrosti sledi tiru krožnice.
Pri tem pa velja, da je pot s, ki jo naredi točka na obodu kroga (glej sliko 1) enaka, kot pri premem enakomernem gibanju:
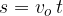
Ta pot je hkrati dolžina krožnega loka krožnice, ki ga opravi telo v času t. Spomnimo se, kako ga izračunamo: dolžina loka je radij r krat kot 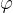 (v radianih), ki ga oklepa:
(v radianih), ki ga oklepa:
Obodna hitrost kroženja je produkt kotne hitrosti in polmera krožnice:
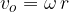
Večkrat smo že omenili, da je hitrost gibanja po kržnici stalna, le smer se menja. Opazujmo, kako se menja smer gibanja med kroženjem!
Na sliki 3 levo sta narisana vektorja hitrosti, ki se razlikujeta le za kot:
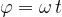
Prestavimo izhodišči obeh vektorjev v isto točko, kot kaže slika 3 desno - da ju bomo lažje razlikovali, ju opremimo z indeksom 1 in 2 (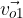 in
in 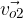 ). Kot med njima je ponovno enak
). Kot med njima je ponovno enak 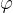 .
.
Vektorju 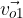 se spremeni smer in postane
se spremeni smer in postane 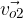 zato, ker se mu vsak trenutek prišteje vektor hitrosti, usmerjen v smeri radija v središče kroženja:
zato, ker se mu vsak trenutek prišteje vektor hitrosti, usmerjen v smeri radija v središče kroženja:
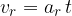
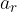 se imenuje radialni pospešek.
se imenuje radialni pospešek.
Izračunajmo radialni pospešek, pri tem si pomagamo s sliko 3 desno. Ponovno uporabimo enačbo za lok krožnice:
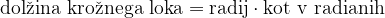
oziroma, če zapišemo to z enačbo:
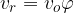
Izračunajmo radialni pospešek:
Radialni pospešek deluje v središče krožnice in povzroča, da se vektor hitrosti po smeri spreminja in je v vsakem trenutku tangenta na krožnico.
Odvisno od podatkov, ki jih imamo, ga izračunamo ga po eni od enačb:
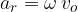
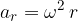
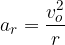
Posebna oblika enakomernega kroženja je kotaljenje.
Oglejmo si pobližje, kaj se dogaja ob kotaljenju in opazujmo točko na obodu kotalečega kolesa (glej sliko 4). Zagotovo lahko rečemo, da točka kroži, saj kolo kroži. A če bi točka samo krožila, bi se po preteku 360° spet znašla na istem mestu - a se ne. Kolo se je vmes premaknilo v smeri kotaljenja naprej. Očitno točka ne samo kroži, temveč se obenem tudi premo giblje. Kotaljenje je zato sestavljeno iz dveh gibanj:
kroženja (rotacije) in
premega gibanja (translacije).
Točka se giblje po krivem tiru, njena hitrost niha med nič v dotikališču kolesa in podlage in dvojno hitrostjo, s katero potuje kolo. V vsaki legi je enaka vektorski vsoti obeh hitrosti, rotacijske in translatorne (glej sliko 4).
Med enakomernim kotaljenje se telo giblje:
premo in enakomerno,
istočasno pa še enakomerno kroži.
Za lažje razumevanje tega gibanja opazujmo hitrosti točk v treh različnih legah: v točkah A, B in T na sliki 5:
Opišimo dogajanje v točkah:
Točka A
Točka A leži na dotikališču med kolesom in podlago. Tu se seštevata dve hitrosti:
hitrost premega (translacijskega) gibanja 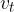 in
in
obodna hitrost kroženja (rotacije) 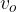 .
.
Če kolo ne spodrsava, sta hitrosti:
po absolutni vrednosti enaki;
usmerjeni nasprotno: bodna hitrost je usmerjena levo, kolo pa se giblje desno.
Obe hitrosti se odštejeta, njuna vsota 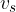 je nič.
je nič.
Točka B
Točka B leži na vrhu kolesa. Hitrost premega (translacijskega) gibanja 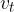 in obodna hitrost kroženja (rotacije)
in obodna hitrost kroženja (rotacije) 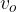 sta:
sta:
absolutno enaki in
enako usmerjeni.
Hitrost 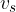 v tej točki je zato enaka dvojni hitrosti gibanja
v tej točki je zato enaka dvojni hitrosti gibanja 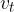 ali dvakratni obodni hitrosti kroženja
ali dvakratni obodni hitrosti kroženja 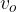 :
:
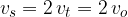
Točka T
Točka T je težišče kolesa. Ta točka se giblje samo premo - ne kroži. Njena hitrost je enaka 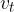 .
.
Če telesu pri kotaljenju ne spodrsava, velja:
obodna hitrost je enaka hitrosti gibanja težišča;
točka na stičišču kotalečega telesa in podlage miruje;
točka na razdalji 2r od podlage se giblje z dvojno hitrostjo gibanja.