Osebne zbirke


V splošnem merjenje pomeni opredelitev lastnosti predmetov oz. ljudi s številskimi vrednostmi. Pri tem merjeno količino primerjamo z osnovno mersko enoto, ki je določena z mednarodnim standardom.
V geometriji je merjenje osnova za določitev velikosti geometrijskih elementov, likov in teles.
Meritev se lahko nanaša na eno (dolžina, širina, višina, globina), dve (ploščina, površina) ali tri (prostornina) prostorske dimenzije, posebna kategorija pa so koti, s katerimi opredelimo velikost ravnine, vpete med dva poltraka.
Dolžina je fizikalna količina, ki pomeni razdaljo med dvema točkama. Splošno jo označujemo z malo črko l, v ravninski geometriji pa jo označimo enako kot daljico, na katero se nanaša (npr. stranice likov z a,b,c,d, diagonale z e,f...)
Ob izrazu dolžina uporabljamo za razdaljo tudi izraze širina, višina in globina.
Osnovna merska enota za merjenje dolžine je meter. Označimo ga z malo črko m.
Poleg osnovne poznamo tudi večje in manjše merske enote za dolžino. Najpogosteje uporabljane so prikazane v naslednji tabeli:
Tekst modre barve v zgornji tabeli predstavlja destiško predpono. Vsaka predpona predstavlja določeno potenco števila 10 s celoštevilskim eksponentom, s katero moramo pomnožiti osnovno enoto, da dobimo enoto s to predpono.
Za pretvarjanje med merskimi enotami za dolžino si lahko pomagamo z naslednjo tabelo:
V prvo vrstico tabele zapišemo dolžino v podani merski enoti, iz druge vrstice pa preberemo isto dolžino v iskani merski enoti.
Uporabo tabele si oglejmo na primerih:
Ploščina je mera za velikost geometrijskih likov.
Tudi ploskve, ki navzven omejujejo geometrijskega telesa, so geometrijski liki. Vsaka od teh ploskev ima svojo ploščino, vsoto teh ploščin pa imenujemo površina geometrijskega telesa.
Osnovna merska enota tako za ploščino kot za površino je kvadratni meter. Označimo ga z 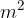 .
.
Poleg osnovne poznamo tudi večje in manjše merske enote za ploščino oz. površino. Najpogosteje uporabljane so prikazane v naslednji tabeli:
Tekst modre barve v zgornji tabeli predstavlja destiško predpono. Vsaka predpona predstavlja določeno potenco števila 10 s celoštevilskim eksponentom, s katero moramo pomnožiti osnovno enoto, da dobimo enoto s to predpono. Ker pri ploščini oz. površini uporabljamo kvadrat osnovne merske enote za dolžino, se tudi predpona kvadrira.
Za pretvarjanje med merskimi enotami za ploščino si lahko pomagamo z naslednjo tabelo:
V prvo vrstico tabele zapišemo ploščino v podani merski enoti, iz druge vrstice pa preberemo isto ploščino v iskani merski enoti.
Uporabo tabele si oglejmo na primerih:
Ploščine običajno ne merimo, temveč jo izračunamo na podlagi merjenja dolžine in uporabe matematičnih enačb.
Dejansko merjenje ploščine lahko med drugim izvedemo z razdelitvijo na enotske kvadrate (z dolžino stranic enako eni enoti) in štetjem teh kvadratov, vendar metoda ni točna, razlaga le-te pa presega vsebino učbenika.
Prostornina je mera za velikost prostora, ki ga zaseda geometrijsko telo.
Osnovna merska enota za prostornino je kubični meter. Označimo ga z 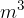 .
.
Poleg osnovne poznamo tudi večje in manjše merske enote za prostornino. Najpogosteje uporabljane so prikazane v naslednji tabeli:
Tekst modre barve v zgornji tabeli predstavlja destiško predpono. Vsaka predpona predstavlja določeno potenco števila 10 s celoštevilskim eksponentom, s katero moramo pomnožiti osnovno enoto, da dobimo enoto s to predpono. Ker pri ploščini oz. površini uporabljamo kvadrat osnovne merske enote za dolžino, se tudi predpona kvadrira.
Za pretvarjanje med merskimi enotami za prostornino si lahko pomagamo z naslednjo tabelo:
V prvo vrstico tabele zapišemo porostornino v podani merski enoti, iz druge vrstice pa preberemo isto prostornino v iskani merski enoti.
Uporabo tabele si oglejmo na primerih:
Prostornine običajno ne merimo, temveč jo izračunamo na podlagi merjenja dolžine in uporabe matematičnih enačb.
Dejansko merjenje prostornine lahko med drugim izvedemo z razdelitvijo na enotske kocke (z dolžino robov enako eni enoti) in štetjem teh kock, vendar metoda ni točna, razlaga le-te pa presega vsebino učbenika.
Ravninski kot je del ravnine, ki ga omejujeta dva poltraka z istim izhodiščem. Več o ravninskih kotih si lahko preberete v poglavju Geometrija v ravnini - osnovni pojmi.
Poleg ravninskih poznamo tudi prostorske kote, a njihova obravnava presega vsebino učne snovi, tako da v tem učbeniku niso zajeti. Zato bomo v nadaljevanju uporabljali enostaven izraz "kot", ob tem pa bomo imeli v mislih ravninski kot.
Kote lahko merimo v stopinjah ali radianih. V prvem primeru je osnovna enota kotna stopinja, v drugem pa radian.
Osnovna merska enota za merjenje ravninskih kotov v stopinjah je kotna stopinja. Označimo jo z " ° ".
Ena kotna stopinja predstavlja kot velikosti 1/360 polnega kota. Polni kot torej meri 360°.
Poleg osnovne poznamo tudi dve manjši merski enoti za kote. Prikazane so v naslednji tabeli:
Merske enote za kote se za razliko od dosedaj obravnavanih enot ne razlikujejo za faktor 10, temveč za faktor 60.
Pretvarjanje med merskimi enotami za merjenje ravninskih kotov v stopinjah najbolje ponazorijo naslednji primeri:
Osnovna (in tudi edina) merska enota za merjenje ravninskih kotov v radianih je radian. Označimo ga z "rad".
Radian je enota brez razsežnosti, zato je običajno ne pišemo.
Kot, merjen v radianih, je definiran s središčnim kotom.
Središčni kot z osnovno enoto radian je namreč enak razmerju med dolžino pripadajočega krožnega loka in polmerom kroga:
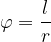
Iz zgornje enačbe pridemo do dveh ugotovitev:
Najprej predpostavimo, da je dolžina krožnega loka enaka celotnemu obsegu kroga:
Ugotovitev 1: Polni kot meri 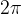 radianov.
radianov.
Sedaj pa predpostavimo, da je dolžina krožnega loka enaka polmeru kroga:
Ugotovitev 2: En radian je središčni kot, ki pripada takemu krožnemu loku, ki je po velikosti enak polmeru kroga.
Ker je nekatere matematične probleme lažje reševati s koti, podanimi v kotnih stopinjah, druge pa s koti, podanimi v radianih, kote preprosto pretvorimo iz ene merske enote v drugo in obratno.
Izpeljimo enačbo za pretvorbo iz stopinj v radiane. Izhajajmo iz dejstva, da polni kot v kotnih stopinjah meri 360°, v radianih pa 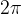 :
:
Iz zgornje enačbe sledi:
Pri pretvorbi iz kotnih stopinj v radiane je potrebno velikost kota pomnožiti s 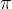 in deliti s 180.
in deliti s 180.
Sedaj pa izpeljimo še enačbo za obratno smer. Zopet izhajajmo iz dejstva, da polni kot v kotnih stopinjah meri 360°, v radianih pa 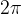 :
:
Glede na zgornjo enačbo lahko zapišemo:
Pri pretvorbi iz radianov v kotne stopinje je torej potrebno velikost kota pomnožiti s 180° in deliti s 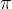 .
.
V naslednji tabeli so navedeni v geometriji najpogosteje uporabljani koti, podani v kotnih stopinjah in radianih:
Povezava med stopinjami in radiani je lepo vidna tudi na t.i. enotski krožnici.
Enotska krožnica je krožnica, ki ima:
središče v koordinatnem izhodišču
polmer ene enote (od tod tudi ime "enotska")
Kote na enotski krožnici prikazujemo na naslednji način:
vrh kota je v koordinatnem izhodišču
en krak kota fiksiramo na pozitivni del abscisne osi
drugi krak kota zavrtimo v matematično pozitivni smeri za vrednost kota
Na naslednjih slikah so na enotski krožnici prikazani ostri, topi in vdrti kot:
Še enkrat zapišimo definicijo kota v radianih:
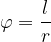
V enotski krožnici je kot 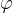 v radianih enak dolžini krožnega loka.
v radianih enak dolžini krožnega loka.
Na spodnjih slikah je prikazana povezava med kotnimi stopinjami in radiani za najbolj značilne kote.
Več o enotski krožnici in njeni uporabi najdete v poglavju Trigonometrija.
Koordinatni sistem pa je predstavljen v poglavju Pravokotni koordinatni sistem.