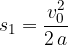Osebne zbirke


V poglavju Enakomerno gibanje smo proučevali telo, ki se giblje s stalno hitrostjo po ravni črti - premici. To gibanje smo imenovali premo enakomerno gibanje.
A v splošnem hitrost gibanja ni stalna, ampak se spreminja s časom. V tem primeru je gibanje neenakomerno.
Na sliki 1 je graf odvisnosti hitrosti telesa od časa za neko neenakomerno gibanje, kjer se telesu hitrost menja po odsekih. Če se mu hitrost veča, govorimo o pospešku, če pa se mu manjša, je pospešek negativen in mu pravimo pojemek.
Kako velik je pospešek (ali pojemek) je odvisno od spremembe hitrosti v opazovanem času:

Enota za pospešek je:
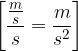
Vrnimo se k sliki 1. Iz matematike vemo, da smerni koeficient oziroma naklon premice izračunamo z obrazcem:
Če pogledamo gornji graf na sliki 1, smo x os označili s t (na x os nanašamo čas), y os pa z v (na y os nanašamo hitrost). Zapišimo še enkrat enačbo za smerni koeficient, z oznakami iz slike 1:
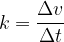
Dobili smo nič drugega kot enačbo (1), kar pomeni, da je pospešek na gornjem grafu slike 1 natanko smerni koeficient posameznih premic. To lahko lepo vidimo v primerjavi s spodnjim grafom: manjši kot je naklon premice (na gornjem grafu), manjši je pospešek (na spodnjem grafu slike 1).
Na spodnjem grafu slike 1 lahko opazimo še:
V intervalu 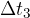 se hitrost ne spreminja, zato je pospešek enak nič.
se hitrost ne spreminja, zato je pospešek enak nič.
V intervalu 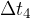 hitrost pada, torej je pospešek negativen. Pravimo mu pojemek.
hitrost pada, torej je pospešek negativen. Pravimo mu pojemek.
Pospešek gibanja je sprememba hitrosti gibanja v opazovanem času:

Pospešek telesa dobimo tako, da opazujemo naklon (strmino) grafa funkcije v(t).
Enota za pospešek je:
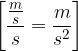
Izračuni v tem poglavju so namenjeni učencem s poglobljenim znanjem. To poglavje lahko bralec izpusti brez škode za razumevanje ostale snovi.
V večini realnih situacij pa se hitrost spreminja zvezno (bolj gladko in ne odsekoma kot na sliki 1). Nekoliko bolj življenjski graf hitrosti in pospeška je prikazan na naslednji sliki:
Najprej opišimo dogajanje na sliki 2: pospešek je v začetku pozitiven in pada. Naklon 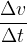 se namreč manjša od časa
se namreč manjša od časa 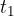 do
do 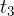 . V času
. V času 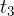 je pospešek enak nič, saj je naklon enak nič. V času
je pospešek enak nič, saj je naklon enak nič. V času 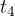 je naklon negativen - graf v(t) namreč s časom pada.
je naklon negativen - graf v(t) namreč s časom pada.
Pospešek take splošne krivulje računamo tako: pri opazovanju naklona krivulje vzamemo dovolj majhne odseke opazovanja 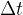 , tako, da lahko smatramo, da se hitrost znotraj
, tako, da lahko smatramo, da se hitrost znotraj 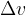 spreminja linearno. A to se zgodi šele takrat, ko se opazovani interval
spreminja linearno. A to se zgodi šele takrat, ko se opazovani interval 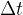 manjša proti neskončno majhni vrednosti (a nikoli ne doseže vrednosti 0). To je pravzaprav kar odvod funkcije v(t) po času t:
manjša proti neskončno majhni vrednosti (a nikoli ne doseže vrednosti 0). To je pravzaprav kar odvod funkcije v(t) po času t:
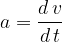
Enačba je zelo podobna enačbi (1), a da bi poudarili, da govorimo o neskončno majhnih razlikah, namesto 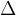 v enačbi uporabimo oznako
v enačbi uporabimo oznako 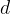 (difference).
(difference).
Enakomerno pospešeno gibanje je posebni primer neenakomernega gibanja, kjer je pospešek a ves čas enak (konstanten). Pri enakomerno pospešenem gibanju se hitrost linearno spreminja s časom.
Izhajamo iz enačbe (1)
Splošna enačba za enakomerno pospešeno gibanje (to je, ko je pospešek a konstanten), se glasi:
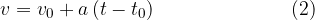
Poglejmo si nekaj posebnih primerov enakomerno pospešenega gibanja.
Obravnavajmo poseben primer enačbe
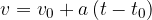
ko je začetna hitrost 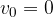 , trenutek, ko pa začnemo meriti gibanje (
, trenutek, ko pa začnemo meriti gibanje (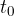 ) pa postavimo na 0. Enačba se preoblikuje v:
) pa postavimo na 0. Enačba se preoblikuje v:
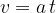
Lahko opazimo, da smo dobili primer linearne funkcije, kjer je prosti člen (n) enak 0; premico začnemo risati v izhodišču, naklon pa določa pospešek a:
Z grafa lahko preberemo, da je v času 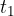 telo dobilo končno hitrost
telo dobilo končno hitrost 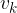 , zato lahko zapišemo pospešek:
, zato lahko zapišemo pospešek:
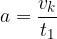
Izračunajmo opravljeno pot. V intervalu 0 do 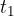 se je hitrost spreminjala od 0 do
se je hitrost spreminjala od 0 do 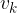 . Telo v tem času opravi pot, ki je enaka produktu srednje hitrosti in časa:
. Telo v tem času opravi pot, ki je enaka produktu srednje hitrosti in časa:
Posplošimo dobljeno enačbo tako, da izrazimo pot s v odvisnosti od poljubnega časa t:
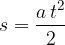
Enačba (4) predstavlja kvadratno funkcijo. Prepotovana pot se pri enakomerno pospešenem gibanju spreminja s kvadratom časa. Poglejmo:
Iz enačbe (3) lahko izrazimo čas 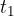 , ko telo opravi pot
, ko telo opravi pot 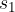 :
:
Končna hitrost pa je:
Posplošimo izraza. Čas, ko telo naredi pot s je:
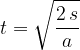
Hitrost v odvisnosti od razdalje paje je:
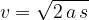
Pri enakomerno pospešenem gibanju z začetno hitrostjo nič, velja, da je:
hitrost v odvisnosti od časa enaka:
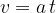
pot, ki jo naredi telo:
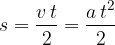
čas, ko naredi pot s:
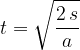
hitrost v odvisnosti od poti s enaka:
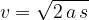
Pri računanju poti, ki jo enakomerno pospešeno telo opravi v času 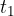 , potrebujemo povprečno hitrost telesa v merjenem času. Ne da bi se na tem mestu spuščali v podrobnejši izračun, samo zapišimo povprečno hitrost telesa, ki je ob začetku merjenja imelo začetno hitrost
, potrebujemo povprečno hitrost telesa v merjenem času. Ne da bi se na tem mestu spuščali v podrobnejši izračun, samo zapišimo povprečno hitrost telesa, ki je ob začetku merjenja imelo začetno hitrost 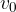 in doseže končno hitrost
in doseže končno hitrost 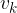 :
:
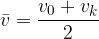
Če je začetna hitrost 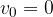 , velja:
, velja:
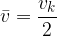
Pot, ki jo opravi enakomerno pospešeno telo, lahko izračunamo tudi s pomočjo grafa; poglejmo si sliko 3. Ploščina pod premico v(t) (ploščina je obarvana z zeleno), je natanko enaka opravljeni poti. Ta ugotovitev velja tudi v splošnem:
Pot pri poljubnem (enakomernem ali neenakomernem) gibanju dobimo pot tako, da izračunamo ploščino pod grafom hitrosti.
Izračunajmo ploščino. Vidimo, da je zelena površina na sliki 3 trikotnik. Ploščina trikotnika pa je osnovnica krat višina polovic. Če to preslikamo na naš primer, ponovno dobimo:
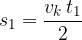
Obravnavajmo poseben primer enačbe
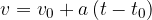
kjer ima telo ob začetku merjenja začetno hitrost 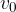 , trenutek, ko pa začnemo meriti gibanje (
, trenutek, ko pa začnemo meriti gibanje (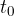 ) pa postavimo na 0. Enačba se preoblikuje v:
) pa postavimo na 0. Enačba se preoblikuje v:
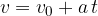
Lahko opazimo, da smo dobili primer linearne funkcije, kjer je prosti člen (n) enak 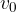 . Kot vemo, nam prosti člen pove, kje premica seka y os: premico začnemo torej risati v točki
. Kot vemo, nam prosti člen pove, kje premica seka y os: premico začnemo torej risati v točki 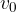 , naklon pa določa pospešek a:
, naklon pa določa pospešek a:
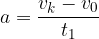
Razdalja, ki jo telo naredi v času 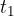 , je enaka ploščini pod grafom hitrosti (glej sliko 5). Sestavljena je iz razdalje, ki bi jo naredilo telo, če bi bi se gibalo s stalno hitrostjo
, je enaka ploščini pod grafom hitrosti (glej sliko 5). Sestavljena je iz razdalje, ki bi jo naredilo telo, če bi bi se gibalo s stalno hitrostjo 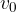 in komponente enakomerno pospešenega gibanja.
in komponente enakomerno pospešenega gibanja.
Enačbo lahko napišemo bolj splošno tako, da izrazimo pot v odvisnosti od poljubnega opazovanega časa:
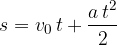
Izračunajmo še hitrost v odvisnosti od razdalje s pri znanem pospešku a in začetni hitrosti 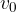 .
.
Pri enakomerno pospešenem gibanju z začetno hitrostjo 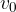 , velja, da:
, velja, da:
lahko hitrost, ki jo telo pridobi v času t, izračunamo s pomočjo naslednjih dveh enačb:
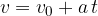
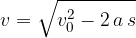
je pot, ki jo opravi telo v času t je:
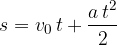
Pri računanju poti, ki jo enakomerno pospešeno telo opravi v času 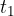 , bomo potrebovali povprešno hitrost telesa v merjenem času. Ne da bi se na tem mestu spuščali v podrobnejši izračun, samo zapišimo povprečno hitrost telesa, ki je ob začetku merjenja imelo začetno hitrost
, bomo potrebovali povprešno hitrost telesa v merjenem času. Ne da bi se na tem mestu spuščali v podrobnejši izračun, samo zapišimo povprečno hitrost telesa, ki je ob začetku merjenja imelo začetno hitrost 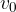 in doseže končno hitrost
in doseže končno hitrost 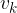 :
:
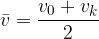
To je dejansko aritmetična sredina med začetno in končno hitrostjo.
Tako kot prej, ko smo izračunali pot, ki jo opravi enakomerno pospešeno telo, lahko tudi zdaj pot izračunamo s pomočjo grafa; poglejmo si sliko 5. Ploščina pod premico v(t) (ploščina je obarvana z zeleno), je natanko enaka opravljeni poti. Ploščina na grafu pa je sestavljena iz pravokotnika in trikotnika:
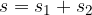
Ploščino obeh likov sta enostavno določljivi; ploščina pravokotnika je:
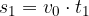
ploščina trikotnika pa:
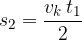
Vstavimo obe ploščini in ponovno dobimo že znano enačbo:
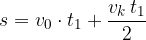
Ob začetku merjenja ima telo začetno hitrost 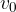 . Ker se telo giblje s stalnim pojemkom, se telesu hitrost zmanjšuje. Pravimo tudi, da telo zavira. Poglejmo, kako izgleda graf hitrosti v odvisnosti od časa (v(t)):
. Ker se telo giblje s stalnim pojemkom, se telesu hitrost zmanjšuje. Pravimo tudi, da telo zavira. Poglejmo, kako izgleda graf hitrosti v odvisnosti od časa (v(t)):
Pospešek takega gibanja je negativen (glej sliko 6). Pravimo mu tudi pojemek. Izračunajmo pojemek:
Enačbe za hitrost in pot so enake kot v prejšnjem poglavju. Upoštevamo le, da je pospešek negativen.
Hitrost v odvisnosti od časa je:
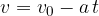
Razdalja v odvisnosti od časa je:
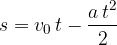
Hitrost v odvisnosti od razdalje pri podanem pospešku pa je:
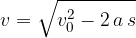
Izračunajmo še čas, ko mu hitrost pade na nič.
Maksimalna razdalja, ki jo naredi, preden se ustavi je enaka ploščini pod grafom hitrosti - slika 5.
Enačbe pri enakomerno pojemajočem gibanju z začetno hitrostjo 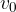 so enake kot enačbe pri enakomerno pospešenem gibanju, le pospešek a spremni predznak in se v enačbah pojavi z minusom (
so enake kot enačbe pri enakomerno pospešenem gibanju, le pospešek a spremni predznak in se v enačbah pojavi z minusom (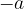 ):
):
hitrost telesa izračunamo s pomočjo naslednjih dveh enačb:
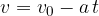
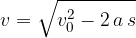
pot, ki jo telo prepotuje v času t je:
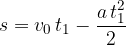
čas, ko se telo ustavi je:
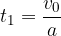
pot zaustavljanja (ali zaviranja) pa je: