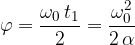Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
Predstavljajmo si majhno telo na krožnici. Telo v začetku miruje, nato pa se prične gibati enakomerno pospešeno. Obodna hitrost telesa narašča s pospeškom, ki je vsak trenutek usmerjen v smeri tangente na krožnico. Pravimo mu tangentni pospešek.
Tangentni pospešek je lahko usmerjen v smeri gibanja telesa. Takrat hitrost telesa narašča (slika 1, levo):
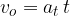
Če je usmerjen v nasprotno smer gibanja telesa, mu hitrost pada (slika 1, desno):
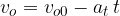
Poleg tangentnega pospeška imamo, podobno kot pri enakomernem kroženju, tudi radialni pospešek. Ta je usmerjen proti središču kroženja in sili telo v krožni tir gibanja.
Slika 1: enakomerno pospešeno kroženje.
Pri enakomerno pospešenem kroženju se telo giblje po krožnici s tangentnim pospeškom:
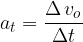
Pri enakomerno pospešenem kroženju kotna hitrost hitrost ni več konstanta. Spreminja se s kotnim pospeškom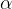 
:
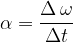
Slika 2: tangentni in kotni pospešek.
Uporabimo enačbo iz enakomernega kroženja, ki povezuje kotno in obodno hitrost;.
Kotna hitrost se spreminja s časom s kotnim pospeškom :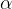
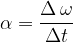
Tangentni in kotni pospešek povezuje enačba:
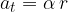
Iz poglavja Enakomerno kroženje se spomnimo povezave med kotom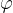 
, ki ga opiše radij medtem, ko telo potuje po krožnici in kotno hitrostjo 
:
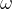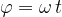
Analogno smo imeli v poglavju Enakomerno gibanje povezavo med potjo, hitrostjo in časom:
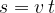
Kaj pa, če se kotna hitrost enakomerno spreminja s časom?
Podoben primer smo imeli pri enakomerno pospešenem gibanju. Takrat se je hitrost enakomerno spreminjala s časom in smo računali pot kot ploščino pod grafom hitrosti v(t). Uporabimo lahko vse enačbe, ki smo jih spoznali pri enakomerno pospešenem gibanju. Zamenjamo le oznake:
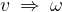
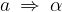
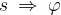
Vzemimo primer, ko kotna hitrost enakomerno narašča od 0 do končne vrednosti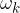 
Slika 3: kot je ploščina pod grafom 
.
Kotna hitrost se spreminja s časom po enačbi:
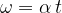
V času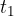 
doseže končno vrednost:
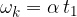
Kot izračunamo kot ploščino pod grafom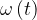 
:
Kotna hitrost je v začetku nič. V času t začne enakomerno naraščati s kotnim pospeškom 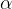. Kot, ki ga opiše zveznica med telesom in središčem kroga, je:
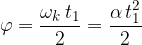
Telo na obodu kroga ima začetno kotno hitrost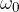 
. V času t = 0 mu začne kotna hitrost enakomerno padati s kotnim pospeškom .
Slika 4: kotna hitrost enakomerno pada s časom.
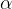Kdaj se telo ustavi?
V času t je kotna hitrost:
Kakšen kot naredi telo med ustavljanjem? Kot je ploščina poda grafom 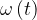(glej sliko 4). V času t naredi kot:
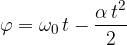
Ustavi se, ko je:
Telo kroži po obodu kroga s kotno hitrostjo 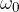ko se začne v času t = 0 ustavljati (pojemajoče krožiti). Kot, ki ga opiše v času t, je:
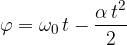
Ustavi se v času:
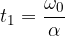
Celoten kot med ustavljanjem je:
