Osebne zbirke
Prijava z e-naslovom
Prijava brez gesla
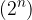skladnih delovZ geometrijsko konstrukcijo razdelimo daljico na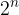 
skladnih delov.
Predpostavimo, da je daljica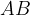 
že narisana:
1. korak
Konstruiramo razpolovišče daljice 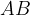in ga označimo s točko 
:
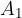Za zgornjo sliko velja:
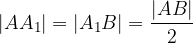
Daljico 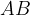smo torej razdelili na dva skladna dela polovične dolžine.
2. korak
Konstruiramo razpolovišče daljice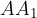 
in ga označimo s točko 
.
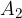Konstruiramo razpolovišče daljice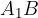 
in ga označimo s točko 
:
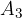Za zgornjo sliko velja:
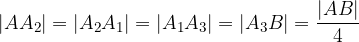
Daljica 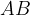je sedaj razdeljena na štiri skladne dele četrtinske dolžine.
Nadaljnji koraki
Postopek, opisan v korakih 1 in 2 ponavljamo, dokler ne pridemo do želenega števila skladnih delov daljice. V vsakem koraku se število skladnih delov daljice 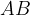podvoji, dolžina posameznega dela daljice pa razpolovi.
V splošnem velja, da lahko z n koraki delitve, daljico 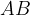razdelimo na 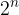skladnih delov z dolžino 
.
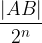Pravkar opisano metodo delitve daljice imenujemo bisekcija in jo bomo v matematiki še srečali pri obravnavi polinomov.
Predpostavimo, da je daljica 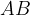že narisana:
1. korak
Z ravnilom narišemo poševen poltrak z izhodiščem v točki A in ga označimo s h.
V šestilo vzamemo poljubno razdaljo.
Šestilo zapičimo v točko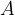 
.
S šestilom zarišemo krožni lok v smeri proč od točke A tako, da seka poltrak h. Tako nastalo presečišče označimo s točko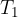 
.
Šestilo zapičimo v točko 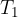in znova zarišemo krožni lok v smeri proč od točke A. Novo nastalo presečišče označimo s točko 
.
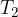Postopek ponavljamo vse do točke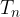 
:
2. korak
Z ravnilom narišemo premico skozi točki 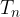in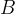 
.
Z ravnilom narišemo vzporednico daljici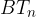 
skozi točko 
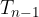. Presečišče vzporednice z daljico 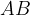označimo z 
.
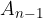Vzporednice daljici 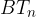narišemo še skozi ostale točke na daljici 
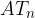in po enaki logiki označimo njihova presečišča z daljico :
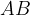Po Talesovem izreku o sorazmerjih za zgornjo sliko velja:
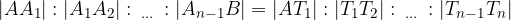
Ker so odseki daljice 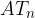skladni, so posledično skladni tudi odseki daljice 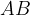. Ob upoštevanju, da ima vsaka od daljic n odsekov, lahko zapišemo, da smo daljico 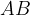razdelili na n skladnih delov dolžine 
.
Omenjeni postopek se lahko uporabi tudi za prikaz ulomka na številski premici, kar ponazarja naslednji primer:
Predpostavimo, da je daljica 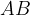že narisana:
1. korak
Z ravnilom narišemo poševen poltrak z izhodiščem v točki A in ga označimo s h.
V šestilo vzamemo poljubno razdaljo.
Šestilo zapičimo v točko .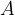
S šestilom zarišemo krožni lok v smeri proč od točke A tako, da seka poltrak h. Tako nastalo presečišče označimo s točko .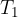
Šestilo zapičimo v točko 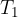in znova zarišemo krožni lok v smeri proč od točke A. Novo nastalo presečišče označimo s točko .
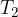Postopek ponavljamo vse do točke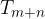 
:
2. korak
Z ravnilom narišemo premico skozi točki 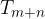in .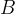
Z ravnilom narišemo vzporednico daljici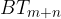 
skozi točko 
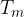. Presečišče vzporednice z daljico 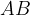označimo z 
:
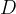Po Talesovem izreku o sorazmerjih za zgornjo sliko velja:
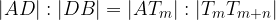
Ker velja sorazmerje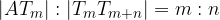 
, posledično velja tudi 
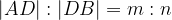in lahko zapišemo, da smo daljico 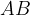smo razdelili v razmerju m:n.
Konstrukcijo bomo izvajali ob predpostavki, da velja
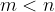
Predpostavimo, da je daljica 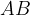že narisana:
1. korak
Z ravnilom narišemo nosilko daljice .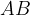
Z ravnilom narišemo poševen poltrak z izhodiščem v točki A in ga označimo s h.
V šestilo vzamemo poljubno razdaljo.
Šestilo zapičimo v točko .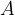
S šestilom zarišemo krožni lok v smeri proč od točke A tako, da seka poltrak h. Tako nastalo presečišče označimo s točko .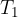
Šestilo zapičimo v točko 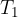in znova zarišemo krožni lok v smeri proč od točke A. Novo nastalo presečišče označimo s točko .
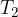Postopek ponavljamo vse do točke :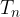
2. korak
Z ravnilom narišemo premico skozi točki 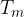in .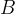
Z ravnilom narišemo vzporednico daljici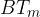 
skozi točko 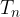. Presečišče vzporednice z nosilko daljice 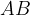označimo z :
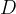Po Talesovem izreku o sorazmerjih za zgornjo sliko velja:
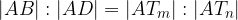
Ker velja sorazmerje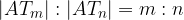 
, posledično velja tudi 
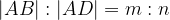in lahko zapišemo, da smo daljico 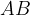podaljšali v razmerju m:n.
