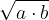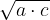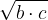Osebne zbirke

Z uporabo izrekov v pravokotnem trikotniku lahko konstruiramo kvadratni koren poljubnega realnega števila. V praksi običajno omejimo na načrtovanje kvadratnih korenov naravnih števil.
Preden se lotimo risanja, ponovimo definicijo Pitagorovega izreka:
Vsota kvadratov katet v pravokotnem trikotniku je enaka kvadratu hipotenuze.
Kvadratni koren števila lahko konstruiramo po Pitagorovem izreku, če ustreza naslednjemu pogoju:
Če je število sestavljeno iz vsote ali razlike kvadratov dveh števil, lahko kvadratni koren tega števila konstruiramo po Pitagorovem izreku.
Uporabo omenjene konstrukcije najbolj nazorno prikažemo na primerih:
Preden se lotimo risanja, ponovimo definiciji:
Višinski izrek: kvadrat višine na hipotenuzo je enak zmnožku pravokotnih projekciji katet na to hipotenuzo.
Evklidova izreka: kvadrat katete je enak zmnožku hipotenuze in pravokotne projekcije katete na hipotenuzo.
Na ta način je možno konstruirati kvadratne korene treh števil naenkrat in sicer:
Če za tri pozitivna števila a, b in c velja
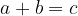
potem lahko po višinskem in Evklidovih izrekih istočasno konstruiramo kvadratne korene