Prijava z e-naslovom
Prijava brez gesla
Pri računanju nas pogosto zanima, če je neko število a deljivo s podanim številom d. Števili bi lahko delili in preverili, če se deljenje izide.
Deljivost z nekaterimi enostavnejšimi števili pa nam ni potrebno preverjati z deljenjem, saj lahko uporabimo hitrejšo metodo. Dovolj je, da preverimo, če število a izpolnjuje tako imenovani kriterij deljivosti s številom d.
Tukaj bomo spoznali, kdaj je poljubno število deljivo z:
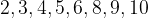
Kriteriji deljivosti so pravila, s pomočjo katerih lahko hitro in enostavno ugotovimo deljivost enega števila z drugim, ne da bi števili dejansko delili.
S kriteriji deljivost ugotavljamo deljivost brez računanja, zgolj z opazovanjem lastnosti števil.
Kriterij deljivosti je enostaven postopek ugotavljanja, če je število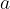 
deljivo s številom 
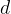. S tem postopkom ugotovimo le, če sta števili deljivi, ne dobimo pa rezultata deljenja.
Kriterije deljivosti uvrščamo v dve skupini glede na deljenec :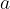
v prvi skupini gledamo zadnjo števko oziroma zadnjih nekaj števk deljenca,
v drugi skupini pa seštevek števk deljenca.
Deljivost v tej skupini ugotavljamo na podlagi zadnje števke oziroma zadnjih nekaj števk.
Če je število a deljivo s številom d, potem je d delitelj števila a, število a pa je večkratnik števila d. Poglejmo najprej en enostaven primer števil, deljivih s 5.
Kot smo spoznali že v uvodu, deljivost s 5 ugotavljamo na podlagi zadnje števke.
Kriterij za deljivost s številom 5:
Število je deljivo s 5, če je zadnja števka enaka 0 ali 5.
Deljivost z 10 ugotavljamo na podlagi zadnje števke.
Kriterij za deljivost s številom 10:
Število je deljivo z 10, če je zadnja števka enaka 0.
Deljivost z 2 ugotavljamo na podlagi zadnje števke. Ta mora biti soda.
Kriterij za deljivost s številom 2:
Število je deljivo z 2, če je zadnja števka enaka 0, 2, 4, 6 ali 8.
Deljivost s 4 ugotavljamo na podlagi zadnjih dveh števk.
Kriterij za deljivost s številom 4:
Število je deljivo s 4, če je njegov dvomestni konec deljiv 4. Ali pa, ko sta zadnji dve števki števila enaki 0.
Deljivost z 8 ugotavljamo na podlagi zadnjih treh števk.
Kriterij za deljivost s številom 8:
Število je deljivo z 8, če je njegov tromestni konec deljiv z 8. Ali pa, če so zadnje tri števke števila enake 0.
Deljivost v tej skupini ugotavljamo na podlagi seštevka števk.
Deljivost s številom 3 ugotovimo tako, da seštejemo vse njegove števke in vsoto delimo s 3. Če pri deljenju s 3 ni ostanka, potem je število deljivo s 3.
Kriterij za deljivost s številom 3:
Število je deljivo s 3, če je vsota njegovih števk deljiva s 3.
Deljivost s številom 9 ugotovimo tako, da seštejemo vse njegove števke in vsoto delimo z 9. Če pri deljenju z 9 ni ostanka, je število deljivo z 9.
Kriterij za deljivost s številom 9:
Število je deljivo z 9, če je vsota njegovih števk deljiva z 9.
Obstaja še nekaj pravil za deljivost, ki ne spadajo v nobeno od zgornjih dveh skupin.
Število 6 lahko zapišemo kot produkt števil 2 in 3:
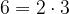
Če je neko število deljivo tako z 2 kot s 3, je deljivo tudi z njunim produktom 6.
V naslednjem primeru preverimo, če je zgornja trditev pravilna.
Kriterij za deljivost s številom 6:
Število je deljivo s 6, če je deljivo tako z 2 kot s 3.
