Osebne zbirke


Logaritemske enačbe so enačbe v katerih neznanka nastopa v logaritmandu ali v osnovi logaritma. Z logaritemsko enačbo se srečamo, kadar želimo izračunati presečišče grafa logaritemske funkcije s katero koli drugo funkcijo (linerano, kvadratno, eksponentno...)
Logaritemske enačbe razlikujemo glede na postopek s katerim jih rešimo.
Na koncu reševanja vedno naredimo preizkus, saj morata biti v začetni enačbi logaritmand in osnova pozitivni realni števili, osnova pa še različna od 1.
Z logaritmiranjem se rešujejo enačbe tipa:
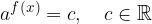
Enačbo lahko logaritmiramo z logaritmom poljubne osnove. Če je mogoče, naj bo osnova logaritma enaka osnovi potence. Ponavadi logaritmiramo z osnovo 10 ali z osnovo e, saj imamo ta dva logaritma na žepnem računalu in tako najlažje izračunamo približek rešitve.
Preproste logaritemske enačbe rešujemo z definicijo:
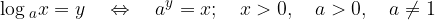
Pri reševanju naslednjih logaritemskih enačb bomo uporabljali pravila za logaritmiranje
Če se v enačbi pojavi več logaritmov z različnimi osnovami, enačbo najprej preoblikujemo v tako obliko, da imajo vsi logaritmi enake osnove. Za novo osnovo izberemo najmanjšo med podanimi osnovami.
Z uvedbo nove neznanke rešujemo logaritemske enačbe višje stopnje in enačbe v katerih logaritem nastopa v obliki algebrskega ulomka. Nova enačba je bolj pregledna in lažje rešlijva.
Kadar logaritemske enačbe ne moremo rešiti z nobenim od že napisanih načinom, jo rešimo grafično. Enačbo, ki jo rešujemo preuredimo tako, da na obeh straneh nastopata funkciji, ki ju znamo narisati. Sledi risanje obeh funkcij v isti koordinatni sistem. Rešiteve naše enačbe so abscise točk, v katerih se grafa sekata. Rešitev potrdimo še z računskim preizkusom.
Logaritemske neenačbe so neenačbe, v katerih neznanka nastopa v logaritmandu logaritma. Neenačbe običajno rešujemo grafično, kar pomeni da narišemo oba grafa, ki v neenačbi nastopata. Enostavnejše neenačbe lahko rešimo tudi računsko.