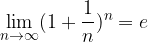Osebne zbirke


Zaporedje je neskončno, če nima zadnjega člena oz. se njegovi členi nadaljuje v neskončnost. V matematiki so neskončna zaporedja pogosta, mnoge med njimi poznamo že dolgo časa: zaporedje naravnih števil, zaporedje sodih/lihih števil, zaporedje kvadratov naravnih števil itd.
Zaporedja so lahko neskončna, a vseeno omejena z neko mejo oz. se členi zaporedja približujejo istemu številu. V tem poglavju si bomo pogledali kako prepoznati tako zaporedje in zapisati njegove lastnosti.
Pogosto lahko opazimo, da neskončno veliko členov poljubnega zaporedja leži v okolici neke točke. Pravimo, da je tako neskončno zaporedje omejeno, in da zanj obstaja neko tako realno število, h kateremu se približujejo vrednosti njegovih členov. Preden si podrobneje ogledamo obstoj in lastnosti tega realnega števila, najprej spoznajmo okolico (neke) točke.
Z okolico točke smo se srečali že pri limiti funkcije, kjer smo spoznali, da velja:
Okolica poljubne točke a je odprt interval  .
.
Okolico točke imenujemo  - okolica točke a in jo označimo z oznako
- okolica točke a in jo označimo z oznako 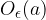 . Število a je središče okolice, pozitivno število
. Število a je središče okolice, pozitivno število  pa imenujemo polmer okolice.
pa imenujemo polmer okolice.
Spoznali smo enega izmed treh načinov kako lahko zapišemo  - okolico točke a. Spoznajmo še druga dva.
- okolico točke a. Spoznajmo še druga dva.
 - okolico točke a lahko, poleg zapisa z intervalom, zapišemo še na dva načina:
- okolico točke a lahko, poleg zapisa z intervalom, zapišemo še na dva načina:
kot sestavljeno neenačbo: 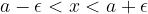 ,
,
kot absolutno vrednost: 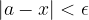
Vemo, da je okolica točke poljubno širok odprt interval, njegova širina oz. širina okolice točke pa je odvisna od vrednosti števila 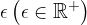 . Običajno za
. Običajno za  vzamemo zelo majhno število, še posebej ko želimo nekaj dokazati.
vzamemo zelo majhno število, še posebej ko želimo nekaj dokazati.
Širina  - okolice je interval širine
- okolice je interval širine 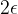 .
.
Pri zaporedjih pogosto opazimo, da mnogo njegovih členov leži v okolici neke točke. Oglejmo si podrobneje neko tako zaporedje.
Vzemimo zaporedje s splošnim členom 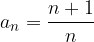 in zapišimo nekaj njegovih členov:
in zapišimo nekaj njegovih členov:
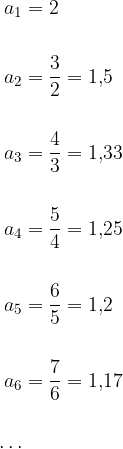
Očitno je dano zaporedje omejeno navzgor, kjer je njegova zgornja meja enaka prvemu členu zaporedja, 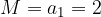 .
.
Če nadaljujemo z zapisovanjem členov danega zaporedja, opazimo, da se členi danega zaporedja približujejo številu 1:
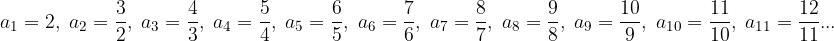
Opazujmo okolico števila 1, katere polovična širina je enaka 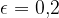 (glej Slika 1, rdeča barva). Očitno je peti člen
(glej Slika 1, rdeča barva). Očitno je peti člen  še izven okolice
še izven okolice 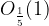 , medtem ko je šesti člen
, medtem ko je šesti člen 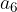 , in vsi ostali, ki mu sledijo, že znotraj te iste okolice.
, in vsi ostali, ki mu sledijo, že znotraj te iste okolice.
Opazujemo še okolico števila 1 pri 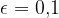 (glej Slika 1, zelena barva). Očitno je tokrat deseti člen
(glej Slika 1, zelena barva). Očitno je tokrat deseti člen 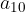 izven okolice
izven okolice 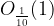 , enajsti člen
, enajsti člen 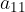 , in vsi ostali, ki mu sledijo, pa so že znotraj
, in vsi ostali, ki mu sledijo, pa so že znotraj  - okolice.
- okolice.
Preverimo naša opažanja še z izračunom. Ali res velja, da 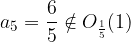 in
in 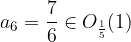 ?
?
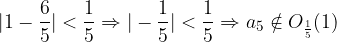
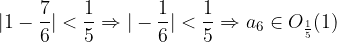
Preverimo še za okolico 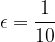 . Ali res velja
. Ali res velja 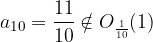 in
in 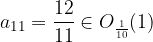 ?
?
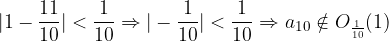
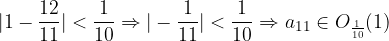
Sklepamo, da ne glede na to kolikokrat zmanjšamo okolico števila 1, vedno obstaja neka taka vrednost spremenljivke N, za katero velja, da se od nje naprej v  - okolici števila 1 nahaja neskončno mnogo členov zaporedja, izven te okolice pa le končno mnogo. Oziroma drugače povedano, zunaj
- okolici števila 1 nahaja neskončno mnogo členov zaporedja, izven te okolice pa le končno mnogo. Oziroma drugače povedano, zunaj  - okolice števila 1 lahko leži le končno mnogo členov zaporedja.
- okolice števila 1 lahko leži le končno mnogo členov zaporedja.
V danem zaporedju 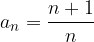 veljajo te lastnosti za število 1, zato število 1 imenujemo limita zaporedja.
veljajo te lastnosti za število 1, zato število 1 imenujemo limita zaporedja.
Zapišimo definicijo limite zaporedja.
Število a je limita neskončnega zaporedja 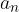 , če za vsako še tako majhno pozitivno število
, če za vsako še tako majhno pozitivno število  obstaja tako naravno število N, da za vsak
obstaja tako naravno število N, da za vsak 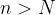
 velja:
velja:
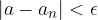
Limito neskončnega zaporedja zapišemo na naslednji način:
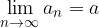
Torej, v danem zaporedju 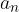 bi limito zaporedja zapisali kot:
bi limito zaporedja zapisali kot:
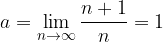
Če ima zaporedje limito, pravimo, da zaporedje konvergira in ga imenujemo konvergentno zaporedje.
Vsako naraščajoče in navzgor omejeno zaporedje je konvergentno (ima limito). Analogno velja tudi za padajoče in navzdol omejeno zaporedje.
Tipičen primer konvergentnega zaporedja je konstantno zaporedje, saj je očitno, da se v poljubni  - okolici konstante vedno nahajajo vsi členi zaporedja.
- okolici konstante vedno nahajajo vsi členi zaporedja.
Velja tudi, da je vsako geometrijsko zaporedje 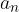 s količnikom
s količnikom  konvergentno zaporedje.
konvergentno zaporedje.
Zaporedje, ki ni konvergentno in nima limite, imenujemo divergentno zaporedje.
Vsako aritmetično zaporedje 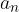 z diferenco različno od nič,
z diferenco različno od nič, 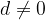 , je divergentno zaporedje.
, je divergentno zaporedje.
Vsako geometrijsko zaporedje 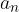 s količnikom enakim - 1,
s količnikom enakim - 1, 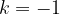 je divergentno in alternirajoče zaporedje.
je divergentno in alternirajoče zaporedje.
Vsako geometrijsko zaporedje 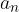 s količnikom
s količnikom  je divergentno zaporedje.
je divergentno zaporedje.
Oglejmo si podrobneje eno izmed zaporedij iz zgornjega zgleda s splošnim členom 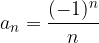 :
:
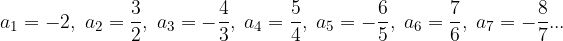
Ponazorimo zaporedje na številski premici:
Vidimo, da se členi zaporedja približujejo dvema različnima številoma, številu 1 in -1, ki pa NISTA limiti zaporedja. Kako to?
Velja, da je neko število limita zaporedja, če od nekega člena dalje VSI členi zaporedja ležijo znotraj poljubno majhne okolice tega števila (limite).
Vzemimo poljubno majhno okolico števila -1 (glej Slika 2, zelena barva). Iz slike razberemo, da peti člen zaporedja leži znotraj okolice, medtem ko naslednji člen, šesti člen, leži že zunaj okolice. Očitno definicija za limito ne velja za število -1 in zato število res ni limita zaporedja.
Vzemimo še poljubno okolico števila 1 (glej Slika 2, zelena barva). Ponovno lahko iz slike razberemo, da je šesti člen del okolice števila, sedmi člen pa že leži zunaj okolice. Očitno tudi število 1 ni limita zaporedja.
Kot smo že v prejšnjem zgledu sklepali, je dano neskončno zaporedje divergentno in brez limite, ima pa dve stekališči, in sicer števili 1 in -1.
Za zaporedja veljajo naslednje trditve, ki se nanašajo na stekališča:
Stekališče zaporedja je število a, ki ima v poljubni  - okolici točke, neskončno mnogo členov danega zaporedja.
- okolici točke, neskončno mnogo členov danega zaporedja.
Limita zaporedja je tudi stekališče zaporedja, obratno pa v splošnem ne velja.
Omejeno neskončno zaporedje ima vsaj eno stekališče (Weierstrassov izrek).
Če ima zaporedje več stekališč, potem zagotovo nima limite.
Za računanje z limitami konvergentnih zaporedij veljajo naslednja pravila:
Limita konstante je konstanta:
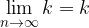
Limita zaporedja 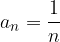 je enaka 0:
je enaka 0:
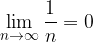
Limita vsote je enaka vsoti limit:
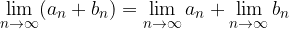
Limita razlike je enaka razliki limit:
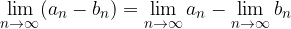
Limita produkta konstante in zaporedja je enaka limiti zaporedja, pomnoženi s konstanto:

Limita produkta je enaka produktu limit:
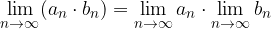
Limita kvocienta je enaka kvocientu limit, če je limita delitelja različna od nič in velja 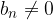 za vsako naravno število:
za vsako naravno število:
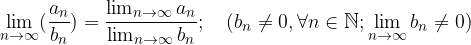
Limita geometrijskega zaporedja 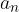 s količnikom
s količnikom 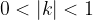 je za vsako naravno število enaka 0:
je za vsako naravno število enaka 0:
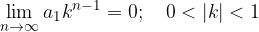
Limita n-tega korena zaporedja 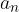 je enaka 0 za vsak člen, ki je večji od 0:
je enaka 0 za vsak člen, ki je večji od 0:
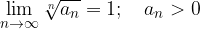
Z neskončnim zaporedjem in limitami povezujemo tudi iracionalno število  , imenovano Eulerjevo število po švicarskem matematiku, fiziku in astronomu Leonhardu Eulerju.
, imenovano Eulerjevo število po švicarskem matematiku, fiziku in astronomu Leonhardu Eulerju.
Število  poznamo že iz poglavja Logaritmi, kjer smo ga spoznali kot osnovo za naravni logaritem, in ugotovili, da je njegova vrednost približno enaka:
poznamo že iz poglavja Logaritmi, kjer smo ga spoznali kot osnovo za naravni logaritem, in ugotovili, da je njegova vrednost približno enaka:
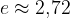
Eulerjevo število  lahko izrazimo z limito:
lahko izrazimo z limito: