Prijava z e-naslovom
Prijava brez gesla
Zrcalo je gladka površina (npr. sploliran aluminij, srebro itd), ki odbija večino vpadne svetlobe. Pri tem velja zakon odboja: kot vpadnega žarka je enak kotu odbitega žarka.
Slika predmeta, ki jo dobimo s pomočjo zrcaljenja je lahko realna ali navidezna. V skicah bomo zato žarke, ki dajo realno sliko označevali s polno črto, navidezne žarke pa s prekinjeno črto. Kaj je realna in kaj je navidezna slika predmeta bomo spoznali na konkretnih primerih.
Za preslikavanje uporabljamo ravno, konkavno ali konveksvo zrcalo.
Največkrat uporabljamo ravno zrcalo. Če se pogledamo v ravnem zrcalu je naša zrcalna slika navidezna (slika 1). Realni žarki sicer izhajajo iz posamezne točke telesa in se na zrcalu odbijajo po zakonu odboja, mi pa vidimo žarke, ki izhajajo iz navidezne slike predmeta - označimo jih črtkano. Zdi se nam namreč, kot da je naša slika za zrcalom.
Slika 1: zrcaljenje človeka v ravnem zrcalu.
Kot zanimivost lahko omenimo, da je pogoj, da se vidimo v zrcalu v celoti ta, da je višina zrcala enaka polovični višini človeka in da je zrcalo nameščeno tako, da je zgornji rob na višini vrha njegove glave (rdeče obarvan pravokotnik - "zrcalo" na sliki 1). Realni žarek, ki izhaja od stopala (najnižje točke) se odbije od zrcala ravno še v točki, kjer se zrcalo začne; pri tem stopalo - točka odboja - oči tvorijo enakokrak trikotnik (glej sliko 1).
Kakšno je konkavno zrcalo?
Pogosto si težko zapomnimo ali je konkavno vbočeno ali izbočeno zrcalo. Eden izmed trikov kako povežemo konkavno zrcalo z vbočenostjo je, da v vbočeno konkavno zrcalo lahko nalijemo kavo.
Snop svetlobe, ki vpada v konkavno zrcalo, se po odboju zbira in združi v eno točko, imenovano gorišče. Lahko je tudi obratno - točkasto svetilo, ki ga postavimo v žarišče, da po odboju snop vzporednih žarkov (primer - avtomobilski reflektor).
Slika 2: preslikava točkastega svetila v snop paralelnih žarkov.
Poglejmo sedaj nekaj pojmov in izrazov, ki jih uporabljamo pri vseh zrcalih (ne samo konkavnem) in so naznačeni na sliki 2.
Osnovni pojmi pri obravnavi zrcal:
Središče zrcala imenujemo teme zrcala in ga označimo s točko T.
Optična os je premica, ki gre skozi teme zrcala in je pravokotna na površino zrcalo v točki T.
Gorišče zrcala F je točka, kjer se po odboju sekajo žarki, ki so pred odbojem vzporedni z optično osjo.
Razdalja gorišča od temena zrcala se imenuje goriščna razdalja f.
Pogosto uporabljamo konkavno zrcalo za preslikave predmeta. Predmet velikosti P postavimo na neko razdaljo a pred zrcalo. Na razdalji b od zrcala dobimo sliko velikosti S. Slika je lahko pomanjšana, enako velika ali povečana glede na predmet. Lahko je pokončna ali obrnjena. Če ustvarjajo sliko realni žarki, je slika realna (slika 3), če pa se sekajo navidezni žarki (primer na sliki 6), je slika navidezna.
Slika 3: preslikave konkavnega zrcala.
Ne glede na to, kje je predmet in kakšna je slika, narišemo določene žarke, ki izhajajo iz predmeta in gledamo, kako se žarki na zrcalu odbijajo.
Poimenovanje žarkov v zrcalu:
Osni žarek vpada v smeri optične osi in po odboju ne spremeni smeri , torej potuje nazaj po optični osi. Pri preslikavah vznožje predmeta P in slike S položimo na os in ga zrcalimo kot osni žarek.
Temenski žarek je žarek, ki vpada na teme zrcala pod določenim kotom in se odbije od temeno pod enakim kotom v nasprotno smer.
Žarek, ki je vzporeden z optično osjo (vzporedni žarek) gre po odboju skozi gorišče.
Goriščni žarek, gre skozi gorišče pred odbojem in je po odboju vzporeden z optično osjo.
Če pogledamo sliko 3, je slika S predmeta P realna (sekajo se realni žarki), pomanjšana in obrnjena.
Žarki, ki so vzporedni z optično osjo, se sekajo v točki F, imenovani gorišče (Fokus). Točka se nahaja na optični osi. Razdalja med temenom T in goriščem F se imenuje goriščna razdalja f. Točka O na sliki 4 je središče krogelne kapice.
Slika 4: konkavno zrcalo: žarki vzporedni z optično osjo se sekajo v gorišču.
Goriščna razdalja krogelne kapice je približno enaka polovični dolžini radija za žarke, ki so vzporedni in blizu optični osi. Dokažimo to trditev!
Opazujmo vzporedni žarek, ki se odbije od zrcala v točki P. Radij r na sliki 4 predstavlja pravokotnico na ploskev, kjer se žarek odbije. Velja odbojni zakon: vpadni kot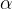 
je enak odbojnemu kotu. Kot med radijem (razdaljo med točkama P - O) in optično osjo je skladen z vpadnim kotom 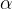, saj sta to izmenična kota. Iz tega sledi, da je trikotnik P - F - O enakokrak trikotnik z osnovnico r. Višina trikotnika seka osnovnico na polovici, torej na r/2.
Iz slike 4 razberemo:
Vidimo, da je v primeru krogelne kapice gorišče odvisno od vpadnega kota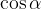 
. Le pri zelo majhnih kotih (majhnih razdaljah žarkov od optične osi) lahko smatramo, da je gorišče točka. V večini primerov se v praksi namesto krogelne kapice uporablja parabola, kjer gorišče ni odvisno od oddaljenosti žarka od optične osi odnosno od širine snopa svetlobe.
Le pri zelo majhnih kotih (majhnih razdaljah žarkov od optične osi) lahko smatramo, da je gorišče krogelne kapice točka.
Goriščna razdalja zrcala s krogelno kapico je enaka polovici radija krogle:
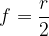
Enačba velja le v primeru, da žarki vpadajo na zrcalo blizu optične osi. Zaradi te omejitve se v praksi običajno uporabljajo parabole. Pri paraboli se vsi žarki, ki so vzporedni z optično osjo sekajo v gorišču.
Enačbi zrcala povezujeta velikost slike in predmeta, njuni oddaljenosti od zrcala in goriščno razdaljo. Enačbi konkavnega zrcala (ki pa veljata tudi za konveksno zrcalo in leče) dobimo z opazovanjem podobnih trikotnikov na sliki 5:
Slika 5: enačba zrcala - žarki tvorijo podobne trikotnike.
Najprej opazujmo oranžno šrafirana trikotnika. Vidimo, da je velikost slike glede na predmet v istem razmerju, kot sta njuni razdalji od temena zrcala:
pri tem je P velikost predmeta, S pa velikost slike.
Opazujmo sedaj s poševimi črtami šrafirana podobna trikotnika. Dobimo:
Enačbi zrcala sta:
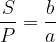
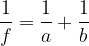
kjer je P velikost predmeta, S velikost slike, a oddaljenost predmeta od zrcala, b oddaljenost slike od zrcala in f goriščna razdalja.
Pri obrnjeni sliki smo vzeli pozitiven S; če bo slika pokončna bo zato S negativen.
Razdalji b in f sta lahko pozitivni ali negativni. Negativna razdalja je vedno razdalja navideznega žarka (glej primer na sliki 6) ali navideznega gorišča, kar bomo ilustrirali pri razpršilnem zrcalu (slika 7).
Konveksno zrcalo sestavlja izbočena krogelna kapica ali parabola. Pri konveksnem ali razpršilnem zrcalu se žarki, ki padajo nanj po odboju razpršijo. Na strani predmeta se ne bodo nikoli sekali. Sekajo pa se navidezni žarki, ki jih prikažemo kot podaljšek realnih odbitih žarkov - slika 6. Označimo jih s prekinjeno črto. Slika je zato navidezna. Iz slike 6 tudi razberemo, da je slika predmeta pokončna in pomanjšana.
Veljata še vedno enačbi zrcala, ki smo ju izpeljali pri konkavnem zrcalu, že v podatkih pa moramo upoštevati, da je goriščna razdalja f negativna. Negativen bo tudi radij zrcala r. Kot rezultat izračuna (glej primer) bomo videli, da bosta negativna tudi b in S.
Slika 7: Konveksno zrcalo.
Slika se nahaja za zrcalom nekje med temenom in goriščno razdaljo. Oddaljenost slike od zrcala je vedno manjša od oddaljenosti predmeta od zrcala. Čim večji je radij, bolj sta absolutni vrednosti razdalj izenačeni:
Za dokaz napišemo enačbo zrcala, kjer upoštevamo, da je f negativen:
Velja tudi, da gre pri veliki oddaljenosti predmeta od zrcala njegova navidezna slika proti gorišču.
Dokaz:
Slika konveksnega zrcala je vedno navidezna, saj se realni žarki na strani predmeta razpršijo. Slika je pokončna, goriščna razdalja in razdalja slike od zrcala pa sta negativni.
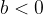
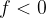
Absolutna vrednost oddaljenosti slike od zrcala b je vedno manjša od oddaljenosti predmeta a:
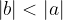
Sledi, da je tudi velikost slike vedno manjša od velikosti predmeta, saj velja enačba:
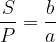
Navidezna slika gre proti gorišču, če gre razdalja predmeta proti neskončnosti.
