Osebne zbirke


Polinom, navadno označen s p(x), je končna vsota neke spremenljivke - navadno jo označimo z x - ki se v vsoti pojavlja v različnih potencah.
V matematičnem jeziku polinom definiramo tako: polinom p(x) stopnje n je realna funkcija, podana s predpisom:
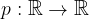
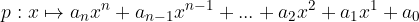
V splošnem polinom zapišemo tako:
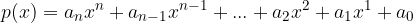
pri čemer so 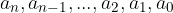 realna števila, ki jim pravimo koeficienti polinoma in velja:
realna števila, ki jim pravimo koeficienti polinoma in velja:
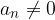
n pa je naravno število. Pri tem imata prvi in zadnji člen svoji imeni:
Vodilni koeficient: koeficient 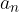 imenujemo vodilni koeficient ali vodilni člen.
imenujemo vodilni koeficient ali vodilni člen.
Prosti člen: koeficient 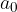 imenujemo prosti člen ali konstantni člen.
imenujemo prosti člen ali konstantni člen.
Polinom, ki ima vse koeficiente enake nič, imenujemo ničelni polinom. Ničelni polinom je:
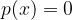
V definiciji polinoma smo omenili, da je polinom realna funkcija.
Iz zapisa 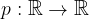 in poznavanja pojma realna funkcija, razberemo, da je:
in poznavanja pojma realna funkcija, razberemo, da je:
definicijsko območje množica realnih števil,
zaloga vrednosti podmnožica realnih števil.
Definicijsko območje lahko zapišemo še z matematičnimi znaki:
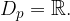
Prav tako pa tudi zalogo vrednosti:
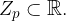
Če želimo izračunati vrednost polinoma, moramo imeti podano vrednost x. Ko imamo podano vrednost x, polinom izračunamo tako, da v polinom vstavimo vrednost. Poglejmo na primerku kako.
Vrednost polinoma za 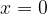 je enaka konstantnemu členu polinoma.
je enaka konstantnemu členu polinoma.
Vrednost polinoma za 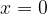 in ničla polinoma sta dva različna pojma.
in ničla polinoma sta dva različna pojma.
Vrednost polinoma za 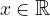 lahko izračunamo tudi s pomočjo Hornerjevega algoritma.
lahko izračunamo tudi s pomočjo Hornerjevega algoritma.
Polinoma sta enaka, kadar imata za vsako realno število enako vrednost. Da pa ne bi računali in primerjali vrednosti dveh polinomov za vsako realno število, bomo uporabili slednji izrek:
Dva polinoma sta enaka samo, če imata enaki stopnji in enake koeficiente pri potencah iste stopnje.