Prijava z e-naslovom
Prijava brez gesla
Vemo, da ima vsak večkotnik enako število stranic, oglišč in notranjih kotov. Pri trikotniku je to število 3, pri štirikotniku 4, petkotniku 5 in tako naprej.
Za pravilne like pa veljajo še dodatne lastnosti, po katerih jih takoj spoznamo in ločimo od nepravilnih.
Pravilni večkotnik je simetričen lik, ki ima vse stranice enako dolge in vse notranje kote enako velike.
Pravilni večkotnik ima skladne vse:
stranice in
notranje kote.
Vsakemu pravilnemu večkotniku lahko očrtamo krožnico.
Očrtana krožnica poteka skozi vsa oglišča večkotnika in se nahaja v celoti izven večkotnika.
Če središče očrtane krožnice povežemo z oglišči pravilnega večkotnika, dobimo toliko skladnih enakokrakih trikotnikov, kolikor oglišč ima večkotnik.
Za skladne enakokrake trikotnike velja:
osnovnica trikotnika je enake dolžine kot stranica večkotnika,
krak trikotnika je enake dolžine kot polmer očrtane krožnice.
Kot v vrhu posameznega enakokrakega trikotnika imenujemo središčni kot.
Vsota vseh središčnih kotov predstavlja polni kot (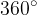
), število skladnih enakokrakih trikotnikov pa je enako številu oglišč večkotnika, zato velja:
Velikost posameznega središčnega kota v pravilnem n-kotniku izračunamo po enačbi:
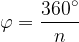
pri čemer n pomeni število oglišč večkotnika.
Če poznamo polmer očrtane krožnice, lahko načrtamo pravilni večkotnik.
Pravilni n-kotnik ima n notranjih kotov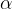 
, ki so enake velikosti.
Velikost posameznega notranjega kota 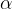v pravilnem n-kotniku izračunamo po enačbi:
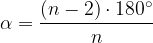
pri čemer n pomeni število notranjih kotov n-kotnika.
Podatek o velikosti notranjega kota lahko uporabimo tudi pri načrtovanju.
Vsakemu pravilnemu večkotniku krožnico lahko tudi včrtamo.
Včrtana krožnica se dotika vseh stranic večkotnika in se nahaja v celoti znotraj večkotnika.
Središči včrtane in očrtane krožnice sovpadata.
Če poznamo polmer včrtane krožnice, lahko načrtamo pravilni večkotnik.
