Osebne zbirke


Tovor želimo potisniti na tovornjak. V ta namen prislonimo ob tovornjak nakladalno rampo. Nakladalna rampa je klanec, ki nam pomaga z manjšo silo spraviti zaboj na tovornjak, kot če bi ga dvignili navpično.
S potiskom rok moramo premagovati dve sili:
silo, ki potiska telo po klancu navzdol; to silo imenujemo dinamična sila klanca 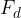 ;
;
silo trenja, ki deluje v nasprotno smer, kot se giblje telo, torej tudi po klancu navzdol.
Kako izračunamo silo trenja in lepenja na klancu? Kaj in kolikšna je dinamična sila? S kakšno silo moramo potiskati tovor v klanec, da se bo gibal enakomerno in premočrtno? Vse to je le nekaj vprašanj, na katera bomo odgovorili v tem gradivu.
Telo z maso m stoji na klancu.
Sila teže telesa 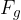 deluje navpično navzdol. Razstavimo jo na dve komponenti:
deluje navpično navzdol. Razstavimo jo na dve komponenti:
statična komponenta: prva komponenta naj bo pravokotna na klanec. Imenujemo jo statična komponenta 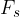
dinamična komponenta: druga komponenta naj bo vzporedna s klancem. Imenujemo jo dinamična komponenta 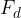 . To je obenem tudi tista komponenta sile teže, ki potiska telo po klancu navzdol.
. To je obenem tudi tista komponenta sile teže, ki potiska telo po klancu navzdol.
Kako bi ju izračunali? Pomagajmo si s sliko 2:
Na sliki 2 opazimo dva podobna trikotnika:
prvi trikotnik predstavlja klanec s katetama d in h ter hipotenuzo s in je obarvan v rumeno. V tem trikotniku je h višina klanca, s pa dolžina klanca. Kot med obema katetama je 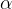 . Ostali koti so vrisani na sliki 2.
. Ostali koti so vrisani na sliki 2.
drugi trikotnik predstavlja trikotnik sile teže 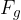 , statične sile
, statične sile 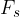 in dinamične sile
in dinamične sile 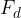 . Ta trikotnik je naznačen z vzporednimi črtami.
. Ta trikotnik je naznačen z vzporednimi črtami.
Trikotnika sta si podobna. V to se lahko prepričamo tako, da pogledamo sliko 2 in ugotovimo skladnost vseh kotov.
Prvi način, kako določiti komponente sile teže je, da napišemo razmerje istoležnih stranic obeh trikotnikov, ki prestavljata geometrijo klanca in sile. Na sliki 2 sta po dve istoležni stranici obeh trikotnikov narisani z isto barvo.
Izračunajmo dinamično komponento:
Izračunajmo statično komponento:
Če je podana strmina klanca s kotom 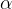 , računamo statično in dinamično komponento sile na klancu s pomočjo kotnih funkcij.
, računamo statično in dinamično komponento sile na klancu s pomočjo kotnih funkcij.
Če pogledamo sliko 2, lahko statično silo izrazimo s pomočjo funkcije kosinus:
Dinamično silo pa izrazimo s pomočjo funkcije sinus:
Pri podanem kotu, ki predstavlja strmino klanca, izračunamo statično in dinamično komponento sile teže s pomočjo kotnih funkcij:
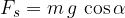
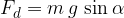
Opazujmo sedaj sile na telo, ki miruje, ali pa se giblje po klancu:
V splošnem na gibanje telesa po klancu najpogosteje vplivajo naslednje sile:
Dinamična sila
Na telo deluje dinamična sila, ki jo prestavimo v težišče telesa. Ta sili telo v gibanje po klancu navzdol:
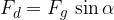
Sila lepenja ali trenja
Druga sila, ki deluje na telo na klancu, je:
sila lepenja (če telo miruje) ali pa
sila trenja (če se telo giblje).
Obe sili izračunamo tako, da množimo koeficient lepenja ali trenja s silo, ki je pravokotna na podlago (normala). Ta sila je enaka in nasprotna statični sili. Sila lepenja deluje v nasprotno smer, kot potiskamo telo. Sila trenja deluje v nasprotno smer gibanja telesa.
Sila lepenja na klancu je:
Sila trenja pa je:
Vlečna sila
Poleg obeh sil lahko deluje na telo tudi vlečna sil 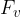 . Ta je lahko usmerjena po klancu navzdol ali navzgor.
. Ta je lahko usmerjena po klancu navzdol ali navzgor.
V smeri gibanja telesa deluje na klancu dinamična sila, usmerjena po klancu navzdol:
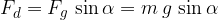
Če telo na klancu miruje je sila lepenja:
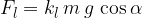
V primeru gibanja telesa je sila trenja:
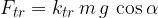
Tudi na klancu velja zakon zakon dinamike in zakon vztrajnosti:
Telo se giblje po klancu enakomerno pospešeno, če je vsota vseh sil, ki delujejo na njega v smeri klanca večja od nič.
Telo se enakomerno giblje po klancu, če je vsota vseh sil, ki delujejo na njega v smeri klanca enaka nič.