Prijava z e-naslovom
Prijava brez gesla
V gradivu Skalarni produkt smo si v splošnem ogledali, kako množimo vektorje med seboj. V tem gradivu pa si bomo ogledali, kako skalarni produkt izvedemo v pravokotnem koordinatnem sistemu.
Skalarni produkt dveh vektorjev, ko je znana njuna dolžina in kot med njima že znamo izračunati. Poglejmo, kako pa bi izračunali skalarni produkt vektorjev, ki so podani s komponentami.
Vektorja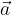 
in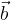 
sta v tridimenzionalnem pravokotnem koordinatnem sistemu podana s komponentami:
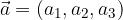
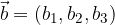
Izpeljimo obrazec za izračun njunega skalarnega produkta:
Skalarni produkt vektorjev 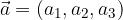in 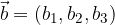v koordinatnem sistemu je enak vsoti produktov posameznih komponent:
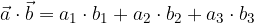
Formula za dolžino vektorja je izpeljana v poglavju Vektorji v pravokotnem koordinatnem sistemu; do enakega rezultata pa lahko pridemo na podlagi spoznanj iz tega gradiva.
Naj bo dan vektor 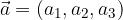. S pomočjo skalarnega produkta lahko zapišemo formulo za dolžino vektorja:
Dolžino vektorja podanega s komponentami 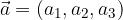izračunamo po formuli:
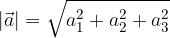
Enotski vektor je vektor, ki ima dolžino 1. Kateremukoli vektorju lahko določimo enotski vektor, uporabljamo pa ga zaradi čisto praktičnih namenov.
Enotski vektor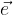 
(poljubnega) vektorja 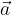določimo tako, da komponente vektorja delimo z njegovo dolžino:
