Osebne zbirke


Vzbudimo val na vpeti elastični vrvi tako, da na eni strani zanihamo vrv. Val potuje do konca vrvi, kjer se odbije. Pri tem pride do seštevanja (superpozicije) vpadnega in odbitega vala.
V posebnem primeru se nam zazdi, da val stoji. Dolžina vrvi ali katerega drugega elastičnega medija je takrat v natančnem sorazmerju z valovno dolžino. Maksimalna amplituda nihanja vrvi je vedno na istem mestu. Vedno na istem mestu je tudi vozel vala, to je točka, kjer vrv miruje.
Stoječe transverzalno valovanje srečamo pri različnih glasbenih inštrumentih s struno (kitara, violina), elastično opno (boben) ali inštrumentih z elastično leseno ali kovinsko ploščico (ksilofon, vibrafon). Struna ali elastična ploščica je lahko:
vpeta na obeh koncih,
vpeta na enem koncu
ali pa sta oba konca prosta - glej sliko 1.

Slika 1: Kitara je primer vpete strune na obeh koncih, nato sledi model inštrumenta, ki ima enostransko vpete elastične jezičke in na koncu ksilofon, ki nima vpetih lesenih ploščic
Predno spoznamo stoječe transverzalno valovanje najprej poglejmo, kako se val na oviri odbije.
Kako se bo val odbil je odvisno od tega, ali je vrv na drugem koncu pritrjena ali pa se lahko giblje - npr. s pomočjo škripca, ki drsi po vodoravni ali navpični prečki.
Če je vrv pritrjena na steno kot kaže slika 2, se val odbije tako, da je postane greben vala po odboju dolina vala in obratno. Pravimo, da se val odbije v protifazi.
Če je vrv na strani odboja pritrjena npr. na gibljiv škripec, kot kaže slika 3, se odbije val tako, da ostaja po odboju greben vala ponovno greben vala in dolina vala ponovno dolina vala. Škripec, na katerega je pritrjena vrv namreč sledi nihanju vrvi. Pravimo, da je odbiti val sofazen z vpadnim valom.
Kaj pa se zgodi, če sinusno zanihamo vrv, ki je vpeta na obeh straneh? Vrv zaniha tako, da zgleda, kot da val miruje. Govorimo o stoječem transverzalnem valovanju. Frekvenca, s katero niha vrv imenujemo lastno frekvenca nihanja napete vrvi.
Raziščimo stoječe valovanje na primeru, ko je dolžina vrvi mnogokratnik valovne dolžine. Na mestu, kjer je vrv vpeta, se val odbije v protifazi. Na prvi pogled zgleda, da se bosta napredujoči in odbiti val izničila. V resnici pa vsak delček vrvi niha s frekvenco 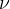 v smeri osi y - glej sliko 4 in z amplitudo, ki je odvisna od razdalje x. Pri površnem opazovanju vidimo samo različne amplitude vala v odvisnosti od razdalje x, razporejene po sinusni funkciji razdalje x. Zgleda, kot da val stoji - slika 4.
v smeri osi y - glej sliko 4 in z amplitudo, ki je odvisna od razdalje x. Pri površnem opazovanju vidimo samo različne amplitude vala v odvisnosti od razdalje x, razporejene po sinusni funkciji razdalje x. Zgleda, kot da val stoji - slika 4.
Pojav lahko raziščemo tudi matematično.
Ta del poglavja je zahtevnejši in namenjen tistim, ki bi želeli vedeti več. Ni bistven za razumevanje nadaljevanja snovi.
V gradivu Potujoče transverzalno valovanje smo spoznali matematični zapis sinusnega potujočega vala.
Vpadni val se širi v smeri osi x proti oviri. Val naj ima amplitudo 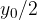 . Nasproti mu prihaja odbiti val enake frekvence in amplitude. Glede na medsebojni fazni pomik se vala seštevata ali odštevata. Ko se bosta seštevala, bo imel greben vala na določeni razdalji x dvojno amplitudo, torej
. Nasproti mu prihaja odbiti val enake frekvence in amplitude. Glede na medsebojni fazni pomik se vala seštevata ali odštevata. Ko se bosta seštevala, bo imel greben vala na določeni razdalji x dvojno amplitudo, torej  . Ko bosta vala v protifazi, bo celotna vrv mirovala. Na določeni razdalji x bo vrv vedno mirovala - to je vozel vala.
. Ko bosta vala v protifazi, bo celotna vrv mirovala. Na določeni razdalji x bo vrv vedno mirovala - to je vozel vala.
Zapišimo sedaj vpadni val - glej Potujoče transverzalno valovanje:
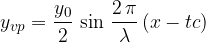
Val zadene ob oviro in se odbije v protifazi (če je vpadni val sinusna funkcija, je odbiti val negativna sinusna funkcija). Širi se v obratni smeri kot vpadni val (torej v smeri -x). Predpostavimo, da gre na mestu odboja val ravno skozi ravnovesno lego:
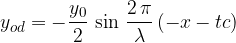
Ker je 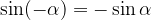 (glej sodost / lihost funkcije sinus) lahko zgornji izraz zapišemo:
(glej sodost / lihost funkcije sinus) lahko zgornji izraz zapišemo:
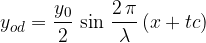
Vpadni in odbiti val se na vrvi seštejeta:
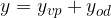
Poglejmo kako se vala seštejeta:
Zapišimo dobljeno enačbo v obliki:
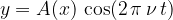
kjer je A(x) amplituda nihanja opazovanega delca na razdalji x od začetka vrvi. Odvisna je samo od razdalje x, ne pa od časa t. To je dejansko ovojnica vala, ki jo vidimo kot stoječi val (glej sliko 4):
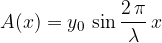
Faktor 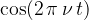 pa predstavlja nihanje delca strune v smeri osi y, ki se dogaja na določeni točki x.
pa predstavlja nihanje delca strune v smeri osi y, ki se dogaja na določeni točki x.
Stoječe valovanje opišemo z enačbo:
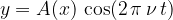
kjer je amplituda vala - ali njegova ovojnica - A(x) odvisna od koordinate x:
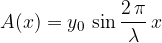
Izračunan val je prikazan na sliki 4. Dejansko je prikazana samo ovojnica vala A(x). Naznačeno pa je tudi nihanje v smeri y osi v obliki vertikalnih premic s puščicami, ki kažejo smer nihanja.
Osnovna frekvenca nihanja napete vrvi je najnižja frekvenca, ko se vzpostavi stoječi val. Vrv lahko zaniha tudi z večkratniki te frekvence. Pravimo jim višje harmonske frekvence.
Osnovna frekvenca nihanja napete vrvi je odvisna od hitrosti valovanja, dolžine vrvi in načina vpetja vrvi.
Vrv napnemo in jo na obeh straneh togo vpnemo. S prsti jo zanihamo. Vrv zaniha z osnovno frekvenco ali katero od višjih harmonskih komponent. Za lažjo predstavo, si lahko predstavljamo, da obravnavamo primer nihanja strune na kitari, kot na sliki 1.
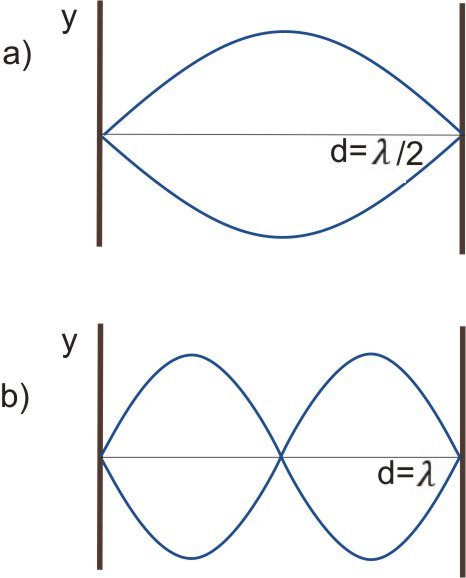
Slika 5: Na straneh vpeta vrv z dolžino d; a) prikazana je osnovna frekvenca nihanja b) prikazana je prva harmonska frekvenca
Iz slike 5 vidimo, da bo pri osnovni frekvenci nihanja dolžina vrvi d enaka polovični valovni dolžini:
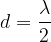
Stoječi val se lahko vzpostavi tudi tako, da se na sredini pojavi valovni vozel (zgornja slika spodaj). Ta delček vrvi miruje. Vrv opiše v tem primeru ravno en cel val:
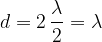
Možno je tudi, da se vzdolž vrvi med nihanjem pojavijo trije vozli:
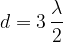
Na splošno velja, da se bo vzpostavil stojni val, ko bo dolžina d vrvi enaka:
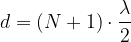
oziroma valovna dolžina:
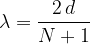
Za N lahko vstavimo 0 ali naravno število.
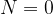 ... Vmes med krajišči vrvi ni vozla.
... Vmes med krajišči vrvi ni vozla.
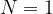 ... Na vrvi je en vozel.
... Na vrvi je en vozel.
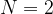 ... Na vrvi sta dva vozla.
... Na vrvi sta dva vozla.
itd.
Valovno dolžino stoječega vala v vrvi, ki je vpeta na obeh koncih, izračunamo z enačbo:

kjer je 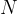 nič ali naravno število,
nič ali naravno število, 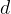 pa je dolžina vrvi.
pa je dolžina vrvi.
Izračunajmo osnovno frekvenco nihanja:
Če je 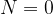 , dobimo osnovno frekvenco nihanja:
, dobimo osnovno frekvenco nihanja:
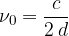
Če vstavljamo 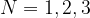 itd. dobimo:
itd. dobimo:
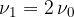 - prvo harmonsko frekvenco (dvakratnih osnovne frekvence),
- prvo harmonsko frekvenco (dvakratnih osnovne frekvence),
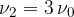 - drugo harmonsko frekvenco (trikratnik osnovne frekvence),
- drugo harmonsko frekvenco (trikratnik osnovne frekvence),
itd.
Namesto vrvi vzemimo elastični jeziček, ga na eni strani togo vpnemo, na drugi strani pa naj prosto niha (glej slika 1 zgoraj). S prsti zanihamo jeziček. Stojni val, ki se vzpostavi, je prikazan na sliki 6 zgoraj.
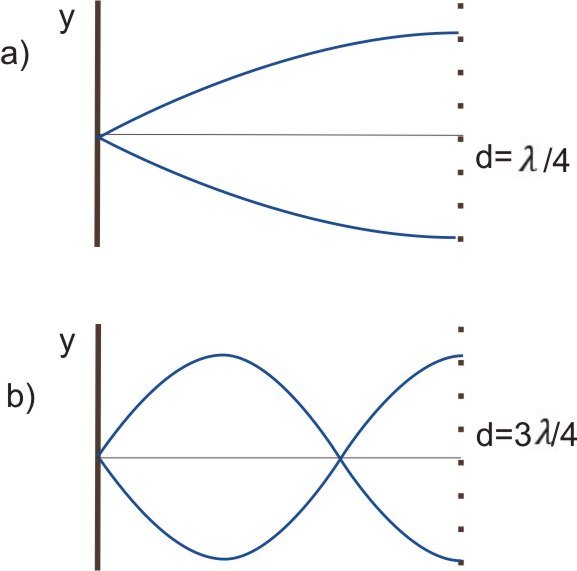
Slika 6 Na eni strani vpet elastični jeziček - a) prikazana je osnovna frekvenca nihanja b) prikazana je tretja harmonska frekvenca
Iz slike 6 vidimo, da bo pri osnovnem nihanju dolžina d ploščice enaka četrtini valovni dolžini:
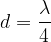
Niha pa lahko tudi s
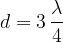
ali
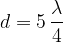
Na splošno velja, da se bo vzpostavil stojni val, ko bo dolžina d:
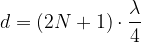
Ali valovna dolžina:
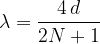
Opazujmo število valovnih vozlov.
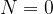 ... na elastičnem traku ni vozla
... na elastičnem traku ni vozla
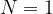 ... en vozel
... en vozel
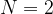 ... dva vozla
... dva vozla
itd.
Valovno dolžino stoječega vala v ploščici, ki je na eni strani vpeta, na drugi pa prosta, izračunamo z enačbo:

kjer je  število vozlov na traku (nič ali naravno število),
število vozlov na traku (nič ali naravno število), 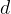 pa je dolžina ploščice.
pa je dolžina ploščice.
Izračunajmo frekvenco nihanja:
Če je 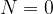 , dobimo osnovno frekvenco nihanja:
, dobimo osnovno frekvenco nihanja:
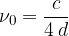
Višje harmonske frekvence dobimo, če vstavljamo 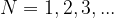
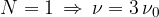 Tretja harmonska komponenta
Tretja harmonska komponenta
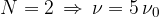 Peta harmonska komponenta
Peta harmonska komponenta
itd.
Vzemimo elastično ploščico (npr. iz lesa ali kovine) in ne da bi jo togo vpeli na podlago, udarimo po njej s kladivcem.
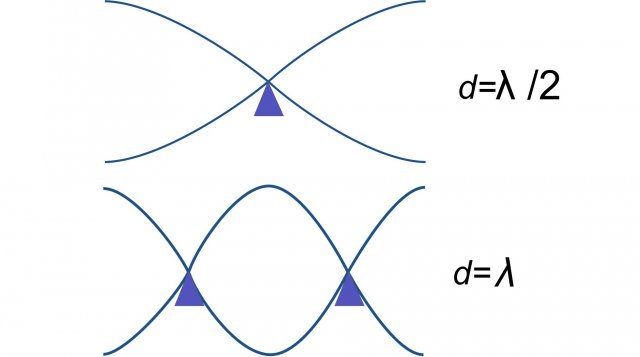
Slika 7 Na obeh straneh nevpeta elastična ploščica. Prikazana je osnovno nihanja, ko se vozel pojavi na sredini ploščice - zgornja slika in nihanje z dvema vozloma.
Ker na koncih ploščica ni vpeta, ima na teh mestih maksimalno amplitudo nihanja. Vmes je eden, dva ali več vozlov, kjer ploščica miruje - odvisno od harmonske frekvence s katero ploščica zaniha.
Na mestu, kjer je vozel, lahko ploščico vpnemo na podlago (primer ksilofon na sliki 1 desno).
Iz slike 7 vidimo, da je pri osnovnem nihanju dolžina d ploščice enaka polovični valovni dolžini:
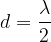
S prvo harmonsko frekvenco bo ploščica nihala, ko bo:
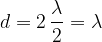
Na splošno velja, da se bo vzpostavil stojni val, ko bo dolžina ploščice d:
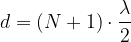
Pri tem je 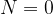 ali naravno število. Valovna dolžina pa je:
ali naravno število. Valovna dolžina pa je:
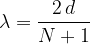
Izračunajmo frekvenco nihanja:
Če je 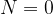 , dobimo osnovno frekvenco nihanja:
, dobimo osnovno frekvenco nihanja:
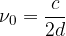
Če zaporedoma vstavljamo 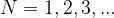 , dobimo prvo, drugo in tretjo harmonsko frekvenco:
, dobimo prvo, drugo in tretjo harmonsko frekvenco:
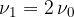
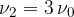
itd.
Nihalo, vpeto na mestih valovnih vozlov niha s frekvencami:
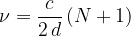
Če vstavimo 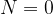 , dobimo osnovno frekvenco nihanja:
, dobimo osnovno frekvenco nihanja:
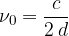
Če vstavimo 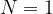 dobimo prvo harmonsko frekvenco,
dobimo prvo harmonsko frekvenco, 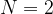 drugo harmonsko frekvenco itd.
drugo harmonsko frekvenco itd.