Osebne zbirke


Trigonometrične enačbe so enačbe, v katerih nastopajo kotne funkcije, argument funkcije (kot) pa je neznanka. Vsako preuredimo na osnovno.
Najosnovnejše enačbe srečamo že, ko iščemo ničle, maksimume in minimume funkcij. Vedno, ko zapišemo rešitev enačbe, moramo upoštevati tudi periodičnost osnovnih funkcij.
Vsaka osnovna trigonometrična enačba ima obliko:
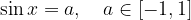
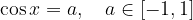
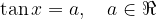
Rešitev enačbe lahko poiščemo na več načinov.
Enačbe tipa
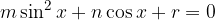
rešujemo po spodnjem postopku:
Enačbo preuredimo v kvadratno enačbo:
Dobili smo kvadratno enačbo. Kvadratno enačbo rešimo z obrazcem:
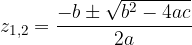
kjer so
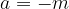
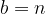
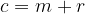
Rešitvi kvadratne enačbe sta tako:
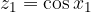
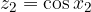
Preostane nam še, da rešimo osnovni enačbi.
Enačbe tipa
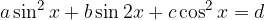
rešujemo po naslednjem postopku:
Ko vstavimo številke, dobimo rešitvi kvadratne enačbe:
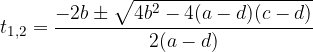
ki sta rešitvi prvotne enačbe.
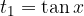
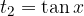
Preostane nam še, da rešimo osnovni enačbi, ki nas pripelje do končnih rešitev enačbe.
Enačbe tipa
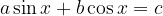
rešujemo po spodnjem postopku:
Enačbo preoblikujemo s pomočjo kotnih funkcij dvojnih kotov v homogeno enačbo:
Ko izračunamo 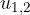 , nam preostane še, da rešimo osnovni enačbi:
, nam preostane še, da rešimo osnovni enačbi:
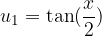
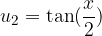
Enačbe tipa
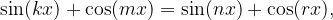
si bomo pogledali na primeru: