Osebne zbirke


V tem poglavju si bomo ogledali kako lahko Odvod uporabljamo za različne namene.
Dana naj bo krivulja 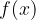 . V točki
. V točki 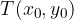 želimo določiti tangento na krivuljo. Ker je tangenta premica, se izračuna lotimo z enačbo za smerni koeficient premice:
želimo določiti tangento na krivuljo. Ker je tangenta premica, se izračuna lotimo z enačbo za smerni koeficient premice:
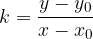
Iz danega obrazca izpeljemo enačbo za tangento na funkcijo 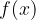 v točki
v točki 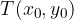 :
:
Enačba tangente na krivuljo 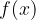 v točki
v točki 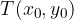 je enaka:
je enaka:
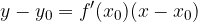
Dana naj bo krivulja 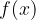 . V točki
. V točki 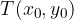 želimo določiti želimo določiti normalo na krivuljo.
želimo določiti želimo določiti normalo na krivuljo.
Vemo, da je tangenta na krivuljo premica, ki se krivulje dotika v dani točki. Normala na krivuljo pa je premica, ki je pravokotna na tangento, poteka pa skozi isto točko, v kateri se tangenta dotika krivulje. Smerni koeficient normale je obraten in nasproten smernemu koeficientu tangente. Torej:
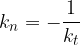
Izračunajmo enačbo normale na funkcijo 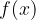 v točki
v točki 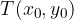 :
:
Enačba normale na krivuljo 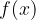 v točki
v točki 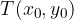 je enaka:
je enaka:
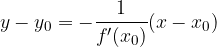
V tem podpoglavju želimo poiskati kot, ki ga oklepa krivulja in abscisa (x os).
Krivulja in tangenta sekata absciso pod enakim kotom:
Zato bomo, ko bomo iskali kot med krivuljo in x osjo, zares iskali kot med tangento na krivuljo in x osjo. Iz teorije vemo, da je tanges naklonskega kota enak smernemu koeficientu tangente:
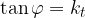
S pomočjo trditve si poglejmo kako izračunamo naklonski kot:
Tangens naklonskega kota je enak odvodu funkcije v presečišču:
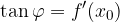
V tem podpoglavju želimo poiskati kot, ki ga oklepa krivulja in ordinata (y os).
Spomnimo: kota sta komplementarna, kadar je njuna vsota 90°. Komplementarnost nam pride zelo prav, saj lahko s pomočjo skice razberemo, da sta kota 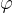 (kot med krivuljo in x osjo) in
(kot med krivuljo in x osjo) in 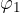 (kot med krivuljo in y osjo) komplementarna:
(kot med krivuljo in y osjo) komplementarna:
Komplementarnost pomeni, da velja:
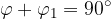
in ker že znamo izračunati kot 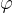 (glej predhodnje poglavje), znamo zato izračunati tudi kot
(glej predhodnje poglavje), znamo zato izračunati tudi kot 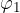 .
.
V tem podpoglavju želimo poiskati kot, ki ga oklepata krivulji v njunem presečišču.
Kot med dvema krivuljama je enak kotu med tangentama na ti dve krivuljo v presečišču krivulj. Za lažje razumevanje si to poglejmo grafično:
Kot med dvema premicama pa tudi že znamo izračnati:
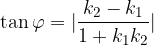
kjer je 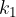 smerni koeficient prve tangente in
smerni koeficient prve tangente in 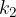 smerni koeficient druge tangente.
smerni koeficient druge tangente.
Ko rišemo grafe funkcije, želimo funkcijo narisati čimbolj natančno. Zato želimo določiti intervale naraščanja / padanja in določiti njene stacionarne točke (stacionarne točke so podrobneje opisane v podpoglavju, ki sledi).
Za lažje razumevanje snovi začnimo s primerom, ki ga že znamo rešiti:
Iz zgornjega primera ugotovimo, da funkcija najprej pada, potem začne naraščati. Ne vemo pa natanko, kje ima točko preobrata; tako so tipična vprašanja, na katera (še) ne znamo odgovoriti:
kje (natančno) funkcija doseže svoj minimum?
kje (natančno) funkcija iz padanja začne naraščati?
ali ima funkcija samo en minimum ali jih ima več?
Odgovore dobimo s pomočjo odvoda. Ob tem bomo pri iskanju točk preobrata potrebovali razumevanje lokalnega maksimuma in lokalnega minimuma; lokalne minimume in lokalne maksimume z eno besedo imenujemo lokalni ekstremi.
Funkcija f ima v točki 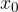 lokalno največjo vrednost ali lokalni maksimum, če so vse funkcijske vrednosti na nekem odprtem intervalu s središčem v
lokalno največjo vrednost ali lokalni maksimum, če so vse funkcijske vrednosti na nekem odprtem intervalu s središčem v 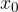 manjše od funkcijske vrednosti
manjše od funkcijske vrednosti  . Največji med lokalnimi maksimumi je globalni maksimum.
. Največji med lokalnimi maksimumi je globalni maksimum.
Funkcija f ima v točki 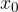 lokalno najmanjšo vrednost ali lokalni minimum, če so vse funkcijske vrednosti na nekem odprtem intervalu s središčem v
lokalno najmanjšo vrednost ali lokalni minimum, če so vse funkcijske vrednosti na nekem odprtem intervalu s središčem v 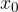 večje od funkcijske vrednosti
večje od funkcijske vrednosti  . Največji med lokalnimi minimumi je globalni minimum.
. Največji med lokalnimi minimumi je globalni minimum.
Opomba: Lahko se zgodi, da ima funkcija v robni točki intervala [a,b] večjo vrednost kot je vrednost v največjem lokalnem maksimumu. Potem ima funkcija globalni maksimum v tej robni točki intervala [a,b]. Enako velja za globalni minimum.
V točkah, v katerih je odvod funkcije pozitiven, funkcija narašča (odvod funkcije je namreč v posameznih točkah enak smernemu koeficientu tangente na krivuljo in če je smerni koeficient pozitiven, funkcija narašča), v točkah, v katerih je odvod funkcije negativen, pa funkcija pada.
Če je 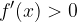 za vsak x z intervala (a,b), potem je funkcija
za vsak x z intervala (a,b), potem je funkcija 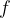 na tem intervalu naraščajoča.
na tem intervalu naraščajoča.
Če je 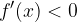 za vsak x z intervala (a,b), potem je funkcija
za vsak x z intervala (a,b), potem je funkcija 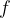 na tem intervalu padajoča.
na tem intervalu padajoča.
V točki 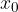 , kjer preide funkcija iz padanja v naraščanje ali iz naraščanja v padanje, ima lokalni ekstrem. V točki lokalnega ekstrema je odvod enak 0:
, kjer preide funkcija iz padanja v naraščanje ali iz naraščanja v padanje, ima lokalni ekstrem. V točki lokalnega ekstrema je odvod enak 0:
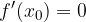
kar pomeni, da ima tangenta na krivuljo smerni koeficient enak nič: je torej vzporedna abscisni osi, kar je lepo razvidno s skice:
Točkam, kjer je odvod funkcije enak nič - tangenta je takrat vzporedna x osi - pravimo stacionarne točke. V stacionarnih točkah se lahko nahaja lokalni minimum / maksimum oziroma prevoj.
Odvedljiva funkcija f ima v točki 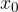 lokalni maksimum, če velja:
lokalni maksimum, če velja:
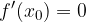
Odvod je levo od točke 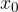 pozitiven, desno od
pozitiven, desno od 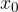 pa negativen.
pa negativen.
Odvedljiva funkcija f ima v točki 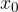 lokalni minimum, če velja:
lokalni minimum, če velja:
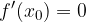
Odvod je levo od točke 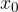 negativen, desno od
negativen, desno od 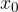 pa pozitiven.
pa pozitiven.
Srečamo pa se tudi s primeri stacionarnih točk, kjer funkcija ne doseže niti minimum niti maksimum. Tem točkam rečemo vodoravni prevoji za katere velja:
Funkcija ima v stacionarni točki 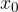 vodoravni prevoj, če v njeni okolici odvod ne spremeni predznaka.
vodoravni prevoj, če v njeni okolici odvod ne spremeni predznaka.
S pomočjo odvoda lahko rešujemo tudi tako imenovane ekstremalne probleme. Ekstremalni problemi so navadno problemi, v katerih določiti količino 1 tako, da bo količina 2 maksimalna / minimalna.