Osebne zbirke


Iz teorije linearne funkcije se spomnimo, da je naklonski kot premice določen s smernim koeficientom k, ki je enak diferenčnemu kvocientu:
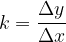
Po definiciji je tangens kota 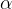 enak:
enak:
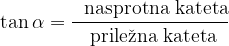
iz spodnje skice pa razberemo, da je to razmerje enako:
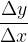
Lahko sklepamo:
Smerni koeficient premice je enak tangensu kota 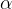 , ki ga premica oklepa z x osjo.
, ki ga premica oklepa z x osjo.
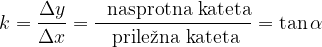
Da bi lahko izračunali kot med premicama, si najprej poglejmo skico:
Vemo, da je vsota notranjih kotov v trikotniku enaka 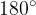 .
.
Vedno računamo ostri kot med dvema premicama, zato uporabljamo absolutno vrednost izraza:
Formula za izračun kota med dvema premicama:
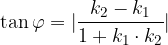
Iz enačbe lahko hitro ugotovimo:
Vzporednost dveh premic
Vemo, da sta premici vzporedni, ko imata enak smerni koeficient:
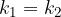
Iz enačbe sledi, da je 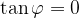 oziroma
oziroma 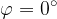 . Kar je rezultat, ki smo ga za dve vzporedni premici pričakovali.
. Kar je rezultat, ki smo ga za dve vzporedni premici pričakovali.
Pravokotnost dveh premic
Premici sta pravokotni, ko za smerna koeficienta velja:
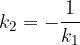
Iz enačbe sledi, da je 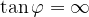 , kar velja, ko je
, kar velja, ko je 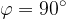 . Kar je rezultat, ki smo ga za dve pravokotni premici pričakovali.
. Kar je rezultat, ki smo ga za dve pravokotni premici pričakovali.