Osebne zbirke

Presek oziroma produkt dogodkov A in B je dogodek, ki se zgodi, kadar se zgodita hkrati dogodka A in B. Označimo na različne načine:
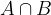
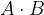
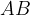
Izraz presek dogodkov je enak izrazu produkt dogodkov in gre za sopomenki ali povedano drugače: produktu dogodkov ustreza presek množic (izidov) obeh dogodkov.
Če je presek dogodkov A in B nemogoč dogodek, pravimo, da sta dogodka nezdružljiva (se ne moreta zgoditi hkrati).
Opazimo, da v splošnem enakost ne velja:
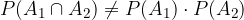
Podobno kot pri računanju verjetnosti vsote, moramo tudi pri računanju produkta dogodkov paziti na to, ali sta dogodka združljiva oz. nezdružljiva.
Dogodka A in B sta neodvisna natanko tedaj, ko je verjetnost produkta dogodkov enaka produktu verjetnosti posameznih dogodkov:
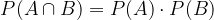
V tem primeru verjetnost enega dogodka ne vpliva na izračun verjetnosti drugega dogodka.
Dogodek B je odvisen od dogodka A, če je verjetnost dogodka B odvisna od tega, ali se je dogodek A zgodil ali ne. Taka dva dogodka sta odvisna dogodka.
Pogojna verjetnost je verjetnost, da se zgodi dogodek B, pod pogojem, da se je zgodil neki drugi dogodek A. Takšno verjetnost označimo s:
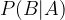
Narišimo si Vennov diagram, v katerem narišemo odvisna dogodka A in B (če sta dogodka odvisna sta prav gotovo tudi združljiva):
Iz diagrama preberemo, da so ugodne možnosti za dogodek B, pod pogojem da se je zgodil dogodek A, možnosti iz produkta dogodkov A in B.
Vsi možni dogodki so enaki vsem ugodnim možnostim za dogodek A, zato pogojno verjetnost izračunamo po naslednji formuli:
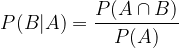
Če to formulo pomnožimo z imenovalcem, dobimo formulo za računanje produkta dogodkov A in B:
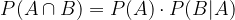
Kadar sta dogodka A in B neodvisna je verjetnost dogodka B, pod pogojem da se je zgodil dogodek A, enaka verjetnosti dogodka B.
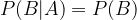
V tem primeru je verjetnost produkta dogodkov A in B enaka produktu verjetnosti dogodkov A in B:
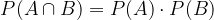
Takšni verjetnosti rečemo tudi brezpogojna verjetnost.