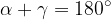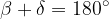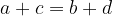Prijava z e-naslovom
Prijava brez gesla
Štirikotnik je geometrijski lik s štirimi oglišči in s štirimi stranicami.
Ker obravnavamo enostavne like, se omejimo na štirikotnike, katerih stranice se stikajo edino v ogliščih in se med seboj ne sekajo. Imenujemo jih enostavni štirikotniki.
Enostavne štirikotnike delimo na:
Konveksni štirikotniki
Za konveksne štirikotnike velja:
Posamezen notranji kot je manjši ali enak 180°.
Vsaka daljica med dvema ogliščema se nahaja znotraj ali na robu lika.
Konveksni štirikotnik
Konkavni štirikotniki
Za konkavne štirikotnike velja:
Natanko en notranji kot je večji od 180°.
Obstaja daljica med dvema ogliščema, katere del se nahaja zunaj lika.
Konkavni štirikotnik
Več o konveksnosti in konkavnosti si lahko preberete v poglavju o množicah.
V učbeniku se bomo posvetili predvsem konveksnim štirikotnikom. Posebej bodo obravnavani:
paralelogram (sem spadajo tudi romb, pravokotnik, kvadrat),
trapez
deltoid
ostali štirikotniki:
tetivni
tangentni in
bicentrični štirikotnik
Paralelogram je štirikotnik z dvema paroma vzporednih stranic. Par predstavljata nasproti si stoječi stranici:
Za stranice in notranje kote paralelograma velja:
Vzporedni stranici sta enake dolžine.
Nasprotna kota skladna.
Sosednja kota sta sokota oz. suplementarna kota.
Ob upoštevanju zgornjih lastnosti skico paralelograma lahko poenostavimo:
Diagonala
Diagonala je daljica, ki povezuje nesosednji oglišči paralelograma.
Paralelogram ima dve diagonali, ki razpolavljata ena drugo. Označimo jih z malima črkama e in f:
Paralelogram je središčno simetričen lik s središčem simetrije v presečišču diagonal.
Višina
Višina paralelograma je pravokotna razdalja med vzporednima stranicama.
Paralelogram ima dve višini. Označujemo ju z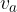 
in 
:
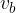Notranji kot
Notranji kot je konveksni kot z vrhom v oglišču paralelograma, njegova kraka pa potekata skozi sosednji oglišči. Notranje kote označujemo z malimi grškimi črkami. Skladna kota pri ogliščih A in C označimo z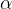 
, skladna kota pri ogliščih B in D pa z 
:
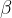Vsota notranjih kotov paralelograma je 360° (polni kot).
Zunanji kot
Zunanji kot je sokot pripadajočega notranjega kota. Zunanji koti so konveksni. Zunanje kote označujemo z malimi grškimi črkami, ki jim dodamo opuščaj - apostrof:
Vsota zunanjih kotov paralelograma je 360° (polni kot).
Romb ima v primerjavi s paralelogramom vse stranice skladne.
Lastnosti romba:
Vse stranice so enake dolžine.
Nasprotna kota skladna.
Sosednja kota sta sokota oz. suplementarna kota.
Diagonali se sekata pod pravim kotom.
Ob upoštevanju zgornjih lastnosti je skica romba naslednja:
Pravokotnik ima v primerjavi s paralelogramom skladne vse kote.
Lastnosti pravokotnika:
Vzporedni stranici sta enake dolžine.
Vsi koti so skladni in merijo 90°.
Diagonali sta skladni in se razpolavljata.
Ob upoštevanju zgornjih lastnosti je skica pravokotnika naslednja:
Kvadrat ima v primerjavi s paralelogramom skladne vse stranice in vse kote.
Lastnosti kvadrata:
Vse stranice so enake dolžine.
Vsi koti so skladni in merijo 90°.
Diagonali sta skladni, se razpolavljata in se sekata pod pravim kotom.
Ob upoštevanju zgornjih lastnosti je skica kvadrata naslednja:
Kvadrat je pravilni štirikotnik, ker so vse njegove stranice enako dolge in vsi njegovi koti med seboj skladni.
Obseg paralelograma se izračuna na naslednji način:
Splošna formula za obseg paralelograma:
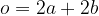
Obseg za posebne primere paralelograma se glasi:
Obseg romba in kvadrata:
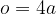
Obseg pravokotnika:
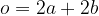
Ploščina paralelograma se izračuna na naslednji način:
Splošna formula za ploščino paralelograma:
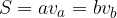
Ploščina za posebne primere paralelograma se glasi:
Ploščina romba:
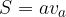
Ploščina pravokotnika:
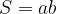
Ploščina kvadrata:
Ko paralelogram razdelimo na trikotnike, lahko v njem uporabljamo trikotniške izreke.
Trapez je štirikotnik z enim parom vzporednih stranic.
Par predstavljata nasproti si stoječi stranici; ti dve stranici imenujemo osnovnici, preostali dve stranici pa imenujemo kraka:
V trapezu sta sosednja notranja kota ob krakih sokota oz. suplementarna kota:
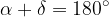
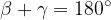
Diagonala
Diagonala je daljica, ki povezuje nesosednji oglišči trapeza.
Trapez ima dve diagonali:
Za diagonali trapeza velja, da je razmerje med odseki delitve diagonal enako razmerju med dolžinami osnovnic:
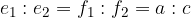
pri čemer je prva diagonala
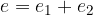
in druga diagonala
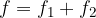
Srednjica
Srednjica je daljica, ki je vzporedna osnovnicama in povezuje središči nevzporednih stranic b in d.
Srednjica m poteka od razpolovišča enega kraka do razpolovišča drugega kraka trapeza
Dolžina srednjice je enaka srednji vrednosti osnovnic a in c:
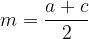
Običajno se srednjico označuje z malo črko s, da pa je ne bomo zamenjevali s polovičnim obsegom trikotnika, ki se prav tako označi z malo črko s, smo si zanjo izbrali oznako m.
Višina
Višina trapeza je pravokotna razdalja med osnovnicama.
Označimo jo z malo črko v:
Notranji kot
Notranji kot je konveksni kot z vrhom v oglišču trapeza, njegova kraka pa potekata skozi sosednji oglišči. Notranje kote označujemo z malimi grškimi črkami , ,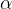 
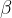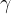in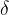 
:
Vsota notranjih kotov trapeza je 360° (polni kot).
Zunanji kot
Zunanji kot je sokot pripadajočega notranjega kota. Zunanji koti so konveksni. Zunanje kote označujemo z malimi grškimi črkami, ki jim dodamo opuščaj - apostrof:
Vsota zunanjih kotov trapeza je 360° (polni kot).
Enakokrak trapez ima v primerjavi s splošnim trapezom skladna kraka in sosednja notranja kota ob osnovnicah.
Lastnosti enakokrakega trapeza:
Kraka trapeza sta enake dolžine.
Sosednja notranja kota ob osnovnicah sta skladna.
Diagonali sta skladni.
Ob upoštevanju zgornjih lastnosti je skica enakokrakega trapeza naslednja:
V Enakokrakem trapezu je v primerjavi s splošnim trapezom eden od krakov pravokoten na osnovnici.
Lastnosti pravokotnega trapeza:
Eden od krakov je pravokoten na osnovnici.
Pravokotni krak je skladen višini trapeza.
Ob upoštevanju zgornjih lastnosti je skica enakokrakega trapeza naslednja:
Obseg trapeza se izračuna na naslednji način:
Splošna formula za obseg trapeza:
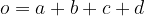
Obseg za posebne primere trapeza se glasi:
Obseg enakokrakega trapeza:
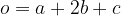
Obseg pravokotnega trapeza:
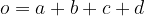
Ploščina trapeza se izračuna na naslednji način:
Splošna formula za ploščino trapeza se glasi:
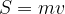
pri čemer je m srednjica trapeza, tj. srednja vrednost osnovnic a in c:
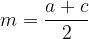
Ploščina za posebne primere trapeza se glasi:
Ploščina enakokrakega trapeza:
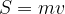
S pomočjo Pitagorovega izreka izrazimo višino s stranicami:
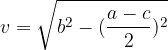
Ploščino enakokrakega trapeza lahko zapišemo tudi kot:
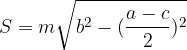
Ploščina pravokotnega trapeza:
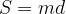
saj je višina enaka stranici d.
Ko trapez razdelimo na trikotnike, lahko v njem uporabljamo trikotniške izreke.
Deltoid je štirikotnik z dvema paroma stranic enake dolžine:
Za stranice in notranje kote deltoida velja:
Deltoid ima dva para sosednjih skladnih stranic.
Kota med neskladnimi stranicami sta enaka.
Ob upoštevanju zgornjih lastnosti skico paralelograma lahko poenostavimo:
Diagonala
Diagonala je daljica, ki povezuje nesosednji oglišči deltoida.
Deltoid ima dve diagonali, ki se sekata pod pravim kotom. Ena izmed diagonal predstavlja simetralo lika in hkrati razpolavlja drugo diagonalo:
Diagonala f predstavlja simetralo lika in hkrati razpolavlja diagonalo e.
Deltoid je osno simetričen geometrijski lik, pri čemer simetralo predstavlja ena od diagonal.
Notranji kot
Notranji kot je konveksni kot z vrhom v oglišču deltoida, njegova kraka pa potekata skozi sosednji oglišči. Notranje kote označujemo z malimi grškimi črkami. Skladna kota pri ogliščih A in C označimo z 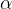, kota pri ogliščih B in D pa z 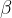oziroma :
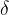Vsota notranjih kotov deltoida je 360° (polni kot).
Zunanji kot
Zunanji kot je sokot pripadajočega notranjega kota. Zunanji koti so konveksni. Zunanje kote označujemo z malimi grškimi črkami, ki jim dodamo opuščaj - apostrof:
Vsota zunanjih kotov deltoida je 360° (polni kot).
Obseg deltoida se izračuna na naslednji način:
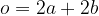
Ploščina deltoida se izračuna na naslednji način:
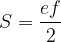
Ko deltoid razdelimo na trikotnike, lahko v njem uporabljamo trikotniške izreke.
Tetivnemu štirikotniku lahko očrtamo krožnico:
Tetivni štirikotnik ima nasprotna kota suplementarna:
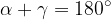
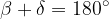
Tangentnemu štirikotniku lahko včrtamo krožnico:
V tangentnem štirikotniku je vsota dolžin dveh nasprotnih stranic enaka vsoti dolžin drugih dveh nasprotnih stranic:
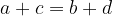
Je hkrati tetivni in tangentni štirikotnik. Imenujemo ga tudi tetivnotangentni štirikotnik.
Tangentnemu štirikotniku krožnico lahko tako očrtamo kot tudi včrtamo:
V bicentričnem štirikotniku veljajo naslednje zakonitosti:
