Prijava z e-naslovom
Prijava brez gesla
Togi premik je poseben primer podobnostne preslikave. Definiramo ga kot:
Togi premik je preslikava, ki ohranja tako velikost kot tudi obliko množice.
Več o preslikavah lahko izvemo v poglavju o množicah.
Med toge premike v ravninski geometriji spadajo:
vzporedni premik
zasuk
zrcaljenje.
Primerjava med njimi je na primeru trikotnika podana na naslednjih slikah:
Vzporedni premik
Zasuk
Zrcaljenje
Predno nadaljujemo, se dotaknimo še pojma simetrije, ki ga bomo potrebovali v nadaljevanju:
Simetrija je v geometriji lastnost geometrijskih likov. Lik je simetričen, če zanj velja, da se njegov del ali lik v celoti pri togem premiku preslika sam vase.
Pri vzporednem premiku se točka togo premakne za določeno dolžino v določeni smeri.
V matematiki količino, določeno z dolžino in smerjo (ter usmerjenostjo) imenujemo vektor, zato lahko definiramo:
Vzporedni premik je predpis, ki poljubni točki T s premikom za vektor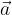 
priredi sliko T':
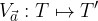
Grafično vzporedni premik ponazorimo na naslednji način:
S pomočjo gornje slike in slike v uvodu lahko razberemo lastnosti vzporednega premika:
vsaki točki pri premiku za določen vektor pripada natančno ena slika in obratno (bijektivna preslikava v obe smeri)
preslikava ohranja naklon premic, daljic, stranic,...
preslikava ohranja dolžino daljic, stranic,...
preslikava ohranja velikost kotov
preslikava ohranja orientacijo likov
Zasuk je predpis, ki poljubni točki T z vrtenjem za kot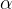 
okoli točke S priredi sliko T' :
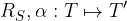
Točko S, okoli katere vrtimo, imenujemo os zasuka. Os zasuka je negibna točka in se pri preslikavi preslika sama vase.
Pri zasuku velja, da vsako točko prenesemo po navidezni krožnici s središčem v točki S. Na tej krožnici se nahajata tako točka T kot tudi njena slika T':
Iz skice lahko razberemo, da za zasuk veljajo naslednje relacije:
Razdalja točke T od točke S je enaka razdalji razdalji točke T' od točke S:
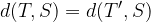
Točki T in T' sta krajišči krožnega loka, ki pripada krožnici s središčem v točki S in polmerom r, za katerega velja:
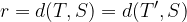
Kot zasuka 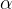je enak središčnemu kotu, kateremu pripada krožni lok s krajišči T in T':
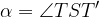
Prav tako lahko s pomočjo gornje slike in slike v uvodu lahko razberemo lastnosti zasuka okoli točke:
vsaki točki pri zasuku okoli določene točke za določen kot pripada natančno ena slika in obratno (bijektivna preslikava v obe smeri)
preslikava NE ohranja naklona premic, daljic, stranic likov,...
preslikava ohranja dolžino daljic
preslikava ohranja velikost kotov
preslikava ohranja orientacijo likov
O sučni simetriji govorimo takrat, ko se original preslika sam vase.
Izrek o sučni simetriji: množica je sučno simetrična, če obstaja točka, okoli katere zavrtimo množico tako, da se množica pri določenem kotu vrtenja preslika vase. To točko poimenujemo središče sučne simetrije.
Pri rotaciji geometrijskih likov velja:
Geometrijski lik, ki se pri vrtenju okoli osi zasuka pri določenem kotu preslika sam vase, je sučno someren. Kot, pri katerem originalni lik in njegova slika sovpadata, imenujemo kot simetrije. Lik ima lahko več kotov simetrije.
Splošno velja, da ima vsak geometrijski lik vsaj en kot simetrije (360 stopinj). Za pravilne n-kotnike pa velja, da imajo med 0 in 360 stopinj še dodatnih (n-1) kotov simetrije.
Zrcaljenje čez točko je predpis, ki poljubni točki T priredi zrcalno sliko T' glede na točko A:
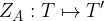
Točko A, čez katero zrcalimo, imenujemo središče zrcaljenja. Središče zrcaljenja se pri zrcaljenju ne premakne; preslika se samo vase.
Pri zrcaljenju velja, da vsako točko preko točke A prenesemo po najkrajši poti, to je po premici, ki poteka skozi vse tri točke, T, A in T':
Za zrcaljenje čez točko veljata naslednji relaciji:
razdalja točke T od točke A je enaka razdalji točke T' od točke A:
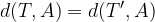
točke T, A in T' so kolinearne.
Zrcaljenje čez točko A lahko definiramo tudi kot zasuk za 180° okoli točke A, torej velja:
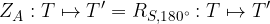
S pomočjo gornje slike in slike v uvodu lahko razberemo lastnosti zrcaljenja čez točko:
vsaki točki pri zrcaljenju čez določeno točko pripada natančno ena slika in obratno (bijektivna preslikava v obe smeri)
preslikava ohranja naklon premic, daljic, stranic likov,...
preslikava ohranja dolžino daljic, stranic likov,...
preslikava ohranja velikost kotov
preslikava ohranja orientacije likov
Zrcaljenje čez točko je identično središčnemu raztegu z vrednostjo koeficienta podobnosti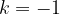 
.
O središčni simetriji govorimo takrat, kot se pri zrcljenju čez točko original preslika sam vase.
Izrek o središčni simetriji se glasi: množica je središčno simetrična, če obstaja točka, čez katero se množica preslika sama vase. To točko poimenujemo središče simetrije.
Pri zrcaljenju geometrijskih likov velja:
Geometrijski lik, katerega del se pri zrcaljenju čez točko A preslika sam vase, je središčno someren. Točko A imenujemo središče simetrije lika.
Zrcaljenje čez premico je predpis, ki poljubni točki T priredi zrcalno sliko T' glede na premico s:
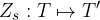
Premico s, čez katero zrcalimo, imenujemo os zrcaljenja. Os zrcaljenja se pri zrcaljenju ne premakne; preslika se sama vase.
Pri zrcaljenju velja, da vsako točko preko premice prenesemo po najkrajši poti, to je pravokotno na premico s:
Za zrcaljenje čez premico veljata naslednji relaciji:
Razdalja točke T od premice s je enaka razdalji točke T' od premice s:
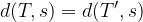
Daljica TT' in premica s sta pravokotni:
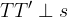
S pomočjo gornje slike in slike v uvodu lahko razberemo lastnosti zrcaljenja čez premico:
vsaki točki pri zrcaljenju čez določeno točko pripada natančno ena slika in obratno (bijektivna preslikava v obe smeri)
za naklon premice velja naslednje:
če premica seka os zrcaljenja pod kotom, različnim od 90 stopinj, se naklon spremeni
če je premica vzporedna ali pravokotna osi zrcaljenja, se naklon ohranja
dolžina daljice se ohranja
velikost kota se ohranja
orientacija lika se spremeni
O osni simetriji govorimo takrat, kot se pri zrcljenju čez premico original preslika sam vase.
Izrek o osni simetriji se glasi: množica je osno simetrična, če obstaja premica, čez katero se množica preslika sama vase. To premico poimenujemo simetrala množice.
Pri zrcaljenju geometrijskih likov velja:
Geometrijski lik, katerega del se pri zrcaljenju čez premico s preslika sam vase, je središčno someren. Premico s imenujemo simetrala lika. Lik ima lahko več simetral.
