Osebne zbirke


V gradivu Enakomerno pospešeno gibanje smo spoznali, da se s pospeškom ali pojemkom spreminja hitrost telesa. Kaj pa je vzrok za pospešek in pojemek?
Vzrok, ki telesu spremeni:
hitrost ali
smer gibanja
je sila, ki deluje nanj.
V zgornjem primeru je nogometaš, s silo svojih nog, deloval na nogometno žogo. Predstavljajmo si, da nogometno žogo zamenjamo s težko medicinsko žogo. V tem primeru bi moral nogometaš na žogi uporabiti večjo silo, da bi jo spravil v gibanje.
V nadaljevanju bomo spoznali, kako so med seboj povezane fizikalne količine:
masa telesa,
sila, ki deluje na telo in
pospešek telesa.
Pri tem bomo obravnavali gibanje, kjer deluje sila v isti ali pa v obratni smeri gibanja.
Vzemimo voziček z maso 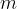 , ki se lahko brez trenja giblje po vodoravni podlagi, kot kaže slika. Upremo se ob voziček in ga s stalno silo
, ki se lahko brez trenja giblje po vodoravni podlagi, kot kaže slika. Upremo se ob voziček in ga s stalno silo 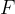 potiskamo pred sabo. Voziček se giblje enakomerno pospešeno s pospeškom
potiskamo pred sabo. Voziček se giblje enakomerno pospešeno s pospeškom 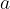 .
.
Sedaj naložimo na voziček tovor tako, da je skupna masa vozička in tovora dvakrat večja, torej 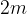 . Z merjenjem sile ugotovimo, da moramo potiskati voziček z dvakratno silo, torej s silo
. Z merjenjem sile ugotovimo, da moramo potiskati voziček z dvakratno silo, torej s silo 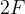 , da se voziček giblje z enakim pospeškom.
, da se voziček giblje z enakim pospeškom.
Pri dvojni masi torej potrebujemo dvakrat večjo silo za enak pospešek. Povejmo ugotovitev še drugače. Pospešek telesa je:
večji, če uporabimo večjo silo - pospešek je premo sorazmeren s silo,
manjši, če ima telo večjo maso - pospešek je obratno sorazmeren z maso.
Ugotovitev zapišimo še v matematični obliki:
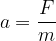
Preverimo pravilnost zgornje enačbe. Vzemimo dvakratno maso in ji damo oznako 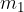 in dvakratno silo z oznako
in dvakratno silo z oznako 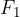 :
:
Vidimo, da se pospešek telesa ne spremeni, če hkrati podvojimo:
maso in
silo.
Preoblikujmo enačbo za pospešek tako, da izrazimo silo 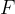 .
.
Enačba:
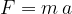
predstavlja drugi Newtonov zakon. Če ga prevedemo v besede, ga razumemo na naslednji način: Telo z maso 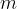 se giblje enakomerno pospešeno s pospeškom
se giblje enakomerno pospešeno s pospeškom 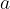 , če nanj deluje rezultanta sil
, če nanj deluje rezultanta sil 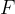 .
.
S pomočjo zgornje enačbe lahko izrazimo enoto za silo z osnovnimi merskimi enotami. To naredimo tako, da v enačbo vstavimo enote za posamezne količine:
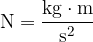
Rezultanta sil pa je lahko:
pozitivna
Pozitivna rezultanta pomeni, da deluje v isto smer, kot se telo giblje. V tem primeru se telo giblje enakomerno pospešeno (pospešek je pozitiven).
negativna
Negativna rezultanta pomeni delovanje sile v nasprotno smer, kot je gibanje telesa. V tem primeru je tudi pospešek negativen. Gibanje je enakomerno pojemajoče.
Drugi Newtonov zakon se glasi:
Naj bo rezultanta vseh sil, ki delujejo na telo enaka 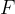 . Potem se se telo z maso
. Potem se se telo z maso 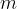 giblje enakomerno pospešeno s pospeškom
giblje enakomerno pospešeno s pospeškom 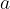 . Velja enačba:
. Velja enačba:
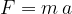
Pozitivna sila deluje v smeri gibanja in telo pospešuje, negativna sila ima obratno smer od gibanja in telo zavira.
Poglejmo si nekaj primerov, ko sila deluje v smeri gibanja telesa. Sila je pozitivna in pospešuje telo.
Poglejmo še primer, ko izračunamo pospešek avtomobila.
Če deluje sila v nasprotno smer gibanja telesa, se telo giblje enakomerno pojemajoče. Poglejmo si nekaj primerov pojemajočega gibanja.
Poglejmo še računski primer, pri katerem izračunamo silo zaviranja.
Teža je sila s katero Zemlja privlači vse predmete. Pojavu pravimo težnost ali gravitacija.
Teža ne deluje samo na Zemlji, pač pa tudi na drugih nebesnih telesih. Sonce, planeti in njihove lune imajo težnost, ki je drugačna od težnosti na Zemlji.
Silo teže bomo označevali z 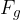 . Indeks g pomeni gravitacija.
. Indeks g pomeni gravitacija.
V gradivu Prosti pad smo videli, da se telo med prostim padanjem giblje enakomerno pospešeno. Pospešek, ki ga ima telo pri prostem padu, smo imenovali pospešek prostega pada ali gravitacijski pospešek in smo mu dali oznako 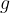 . Znaša približno:
. Znaša približno:
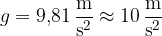
Tudi teža lahko v skladu z 2. Newtonovim zakonom povzroči gibanje telesa.
Napišimo 2. Newtonov zakon:
Dobili smo preoblikovan 2. Newtonov zakon za težo teles. Teža je torej enaka produktu mase in pospeška prostega pada. Ker je pospešek prostega pada približno 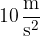 , lahko rečemo, da je teža v Newtonih N številsko deset krat večja od mase v kg.
, lahko rečemo, da je teža v Newtonih N številsko deset krat večja od mase v kg.
Teža ali gravitacijska sila  je sila, s katero Zemlja (ali drugo nebesno telo) privlači vsa telesa. Izračunamo jo kot produkt mase in gravitacijskega pospeška:
je sila, s katero Zemlja (ali drugo nebesno telo) privlači vsa telesa. Izračunamo jo kot produkt mase in gravitacijskega pospeška:
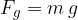
Poglejmo si, kako teža vpliva na telesa:
v mirovanju,
v prostem padu,
na klancu.
Videli bomo, da je od podlage odvisno, kakšno bi gibanje telesa le zaradi njegove teže.
Da telo miruje, mora biti rezultanta vseh sil, ki deluje na telo enaka nič. Če deluje teža 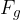 navpično navzdol, mora obstajati še enako velika sila, ki deluje navpično navzgor. To je sila, s katero podlaga deluje na telo. Imenujemo jo sila podlage in ji damo oznako
navpično navzdol, mora obstajati še enako velika sila, ki deluje navpično navzgor. To je sila, s katero podlaga deluje na telo. Imenujemo jo sila podlage in ji damo oznako 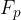 .
.
Če je sila podlage manjša od teže telesa, se telo giblje v smeri njune rezultante, torej navpično navzdol.
Če pa je sila podlage enaka nič (podlage ni), telo prosto pada. Njegovo gibanje je enakomerno pospešeno s pospeškom 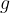 .
.
Na klanec postavimo telo. Poglejmo si, kakšno gibanje povzroča samo teža telesa. Teža deluje navpično navzdol, proti središču Zemlje. Razstavimo jo na dve pravokotni komponenti:
statično,
dinamično.
Statična komponenta teže 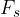 deluje pravokotno na klanec in pritiska telo ob klanec. Klanec pa deluje na telo z nasprotno enako silo
deluje pravokotno na klanec in pritiska telo ob klanec. Klanec pa deluje na telo z nasprotno enako silo 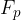 . Sili
. Sili 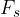 in
in 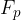 sta uravnovešeni (se odštejeta), zato se telo ne giblje v smeri pravokotno na klanec.
sta uravnovešeni (se odštejeta), zato se telo ne giblje v smeri pravokotno na klanec.
Dinamična komponenta teže 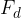 kaže po klancu navzdol. Če na telo ne delujejo nobena druga zunanja sila (trenje, upor, vlečne in potisne sile), potem je
kaže po klancu navzdol. Če na telo ne delujejo nobena druga zunanja sila (trenje, upor, vlečne in potisne sile), potem je 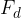 kar rezultanta vseh sil, ki delujejo na telo. Zato v skladu z 2. Newtonovim zakonom povzroča, da se telo giblje enakomerno pospešeno po klancu navzdol. Čim večja je strmina klanca, večja je dinamična komponenta in večji je pospešek.
kar rezultanta vseh sil, ki delujejo na telo. Zato v skladu z 2. Newtonovim zakonom povzroča, da se telo giblje enakomerno pospešeno po klancu navzdol. Čim večja je strmina klanca, večja je dinamična komponenta in večji je pospešek.
Klanec si lahko predstavljamo kot blagi prosti pad. V skrajnem primeru, če je klanec navpičen, gibanje preide v prosti pad.