Osebne zbirke


V poglavju Longitudinalno valovanje zvoka smo spoznali nastanek zvočnega vala: zvočilo pri premiku membrane stisne ali razredči molekule zraka ali pa katere druge snovi, ki prenaša zvok. Zgoščine in razredčine se nato širijo proti sprejemniku. Delci snovi torej vsiljeno nihajo s frekvenco, ki jo določa izvor zvoka.
Energija zvoka je energija nihajočih delcev. Molekule snovi se obnašajo podobno kot prožna vzmet. Ko se stisnejo (povečan tlak), je vsa energija zvoka v prožnostni energiji. S širjenjem molekul se niža prožnostna energija in veča kinetična energija. V ravnovesni legi (to je pri srednjem zračnem tlaku) je vsa energija v kinetični energiji molekul.
Kot pri vzmetnem nihalu, tudi za nihanje molekul v snovi velja, da je celotna energija nihanja enaka vsoti kinetične in prožnostne energije. Celotna energija je konstantna in enaka maksimalni prožnostni ali pa maksimalni kinetični energiji:
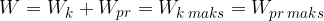
Opazujmo vzdolžno nihanje molekule z maso m. Njena kinetična energija je:
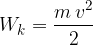
Iz kinetične energije lahko izpeljemo gostoto kinetične energije:
Maksimalna kinetična energija nihanja je pri maksimalni hitrosti:
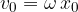
Ko maksimalno hitrost vstavimo v gostoto kinetične energije, dobimo skupno (maksimalno) gostoto energije w. To je tudi skupna gostota zvočne energije:

Vidimo, da je gostota zvočne energije tem večja, čim večja je gostota snovi. Zvok ima zato v kovini veliko večjo energijo kot zvok zraka pri istem odmiku od ravnovesne lege in isti frekvenci.
Zvočni tok (ali moč zvoka) P je njegova energija v opazovanem času:
Če moč delimo s ploskovnim presekom S, dobimo gostoto energijskega toka j:
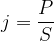
Gostoto energijskega toka izpeljemo iz gornje enačbe:
Gostota energijskega toka je torej gostota energije w, pomnožena s hitrostjo širjenja energije c.
V gornjo enačbo vstavimo enačbo (1):
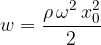
in dobimo gostoto zvočnega toka:
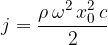
Zvok, ki ga lahko slišimo, se nahaja v območju gostote zvočnega toka med 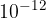 in
in 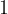 vatom na kvadratni meter:
vatom na kvadratni meter:
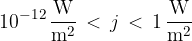
Najnižjo gostoto zvočnega toka, ki jo še slišimo, imenujemo slušni prag. Slušni prag je odvisen od frekvence zvoka. Človeško telo je najbolj občutljivo za frekvenco približno 3 kHz.
Pri ostalih frekvencah, ki jih človek lahko sliši (20 Hz do približno 20 kHz) je potrebna večja gostota zvočnega toka. Prav tako se slišnost zlasti višjih frekvenc niža s starostjo.
Maksimalna gostota zvočnega toka je omejena s pragom bolečine.
Občutek zvoka - to je slušna jakost zvoka - ni sorazmeren gostoti zvočnega toka, pač pa njegovemu logaritemskemu razmerju:
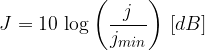
Enota za jakost zvoka je decibel [dB]. 0 dB je spodnji slušni prag in 120 dB prag bolečine.
Iz gornjega zapisa vidimo, da je jakost zvoka logaritemska funkcija. Če pa kot graf želimo premico, moramo na absciso nanesti logaritemske vrednosti. Graf jakosti zvoka je torej linearna funkcija desetiškega logaritma, ki ima v argumentu razmerje med opazovano gostoto zvočnega toka 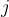 in pragom slišnosti pri
in pragom slišnosti pri 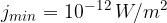 .
.
Zvočnik oddaja zvok, ki vsebuje več frekvenc hkrati. Zvok se preko longitudinalnega valovanja zraka prenaša do našega ušesa. Lahko ga slišimo, zvočno valovanje pa tudi vidimo, npr. tako, da ga posnamemo z mikrofonom in pogledamo na osciloskopu. V tem primeru valovanje zraka pretvorimo v električni signal z enako obliko, kot jo ima zvočni signal. Na osciloskopu tako vidimo obliko vala, to je, kako se val spreminja s časom. Vidimo torej časovno funkcijo odmika od ravnovesne lege x(t) longitudinalnega valovanja zraka, pretvorjeno v električni signal.
V primeru, da gledamo posnetek zvena, vidimo, da je val še vedno periodičen, nima pa sinusne oblike. Vemo že, da nesinusna oblika vala vsebuje višje harmonične komponente, iz slike pa ne vidimo, kolikšna je njihova velikost - glej spodnje primere. Če pa gledamo posnetek šuma, vidimo popolnoma naključno funkcijo časa, ne vidimo pa, katere frekvence vsebuje ta šum in kako so poudarjene.
Za določitev, iz katerih frekvenc je sestavljen zven ali šum, moramo narediti frekvenčno ali spektralno analizo. Naredimo jo lahko neposredno iz podane časovne oblike vala x(t). V ta namen se uporablja nekoliko bolj zapleteno matematično orodje, imenovano Fourierova analiza. Tega matematičnega orodja še ne obvladamo, lahko pa ga kljub temu uporabljamo. Je sestavni del mnogih računalniških programov, namenjenih analizi zvoka.
Rezultati analize so običajno predstavljeni v obliki grafa. Graf ima:
na abscisni osi označimo kotno hitrost ali frekvenco,
na ordinatno os pa lahko izpišemo:
izračunan ali izmerjen delež moči, ki jo ima zvok v ozkem frekvenčnem območju okoli izbrane frekvence:
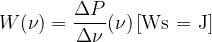
Imenuje se spektralna gostota moči.
gostoto zvočnega toka v ozkem opazovanem frekvenčnem pasu:
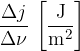
Imenuje se spektralna gostota zvočnega toka.
Največkrat je skala na ordinatni (y) osi grafa spektra izpisana v decibelih - dB. Kaj pa so decibeli? V prejšnjem poglavju smo se naučili, kaj je jakost zvoka, izražena v decibelih. Podobna enačba, kot za jakost zvoka, velja tudi bolj splošno. V našem primeru dobimo skalo v decibelih, če primerjamo spektralno gostoto moči 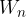 z neka referenčno vrednostjo
z neka referenčno vrednostjo 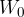 (npr. spektralno gostoto moči osnovnega tona), logaritmiramo in množimo z 10:
(npr. spektralno gostoto moči osnovnega tona), logaritmiramo in množimo z 10:
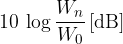
Valovanje zvoka ima lahko:
diskretni spekter
Diskretni spekter ima deleže energije samo pri določenih frekvencah. Diskretni spekter ima npr. zven. V spektru zvena so navpične spektralne črte samo pri frekvencah, ki sestavljajo zven.
zvezni spekter
Zvezni spekter ima neperiodičen val. To je npr. šum ali pok. Oba vsebujeta neskončno število frekvenc. V tem primeru je spekter zvezna funkcija - krivulja ali premica, ki kaže odvisnost 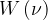 .
.
Spekter zvoka lahko tudi izmerimo. Zato uporabljamo specializirane elektronske inštrumente - spektralne analizatorje ali pa katerega od številnih računalniških programov, namenjenih sintezi zvoka (generator zvoka) in njegovi analizi.